Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có d: −2x + y = 3 ⇔ y = 2x + 3 và d’: x + y = 5 ⇔ y = 5 – x
Xét phương trình hoành độ giao điểm của d và d’: 2x + 3 = 5 – x ⇔ x = 2 3
⇒ y = 5 – x = 5 − 2 3 = 13 3
Vậy tọa độ giao điểm của d và d’ là 2 3 ; 13 3
Suy ra nghiệm của hệ phương trình − 2 x + y = 3 x + y = 5 là 2 3 ; 13 3
Từ đó y 0 – x 0 = 13 3 − 2 3 = 11 3
Đáp án: A

a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm

Bài 2:
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=-x+3\)
\(\Leftrightarrow2x^2+x-3=0\)
\(\Leftrightarrow2x^2-2x+3x-3=0\)
\(\Leftrightarrow2x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot1^2=2\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)
Vậy: Tọa độ giao điểm của (p) và (D) là (1;2) và \(\left(-\dfrac{3}{2};\dfrac{9}{2}\right)\)

a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
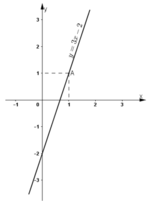
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
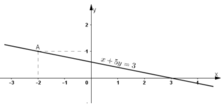
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 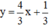
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
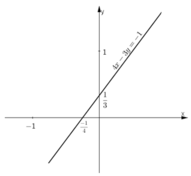
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
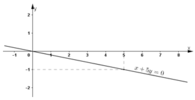
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 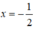
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
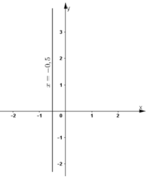
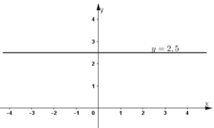
f) 0x + 2y = 5
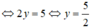
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.

Câu 6 :
Ta có hệ phương trình : \(\left\{{}\begin{matrix}x+2y=n\left(I\right)\\2x-3y=5\left(II\right)\end{matrix}\right.\)
- Từ ( I ) ta có phương trình :\(x+2y=n\)
=> \(x=n-2y\left(III\right)\)
- Thay x = n - 2y vào phương trình (II ) ta được : \(2\left(n-2y\right)-3y=5\)
=> \(2n-4y-3y=5\)
=> \(-7y=5-2n\)
=> \(y=\frac{5-2n}{-7}=\frac{2n-5}{7}\)
- Thay \(y=\frac{2n-5}{7}\) vào phương trình ( III ) ta được : \(x=n-\frac{2\left(2n-5\right)}{7}\)
=> \(x=\frac{7n}{7}-\frac{4n-10}{7}\)
=> \(x=\frac{3n-10}{7}\)
Ta có : \(\left\{{}\begin{matrix}x< 0\\y>0\end{matrix}\right.\) ( IV )
- Thay \(x=\frac{3n-10}{7}\), \(y=\frac{2n-5}{7}\) vào hệ bất phương trình ( IV ) ta được : \(\left\{{}\begin{matrix}\frac{3n-10}{7}< 0\\\frac{2n-5}{7}>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3n-10< 0\\2n-5>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3n< 10\\2n>5\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}n< \frac{10}{3}\\n>\frac{5}{2}\end{matrix}\right.\)
=> \(\frac{5}{2}< n< \frac{10}{3}\)
Vậy để phương trình trên có nghiệm (x, y ) thỏa mãn x <0, y > 0 thì \(\frac{5}{2}< n< \frac{10}{3}\)

a, Cho pt đt (d) có dạng y = ax + b
(d) đi qua N(2;3) => 3 = 2a + b
(d) // y = 2x - 5 <=> \(\left\{{}\begin{matrix}a=2\\b\ne-5\end{matrix}\right.\)
Thay a = 2 ta được : 3 = 4 + b => b = -1 (tmđk )
Vậy ptđt (d) có dạng y = 2x - 1
b, Hoành độ giao điểm tm pt
\(x^2-2x-3=0\)ta có : a - b + c = 0
Vậy pt có 2 nghiệm \(x_1=-1;x_2=3\)
Với x = -1 => y = 1
Với x = 3 => y = 9
Vậy A(-1;1) ; B(3;9)
c, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-5\end{matrix}\right.\)
Ta có : \(A=\left(x_1+x_2\right)^2-3x_1x_2\)
Thay vào ta được :
\(A=4-3\left(-5\right)=19\)
Ta có d: 4x + 2y = −5 ⇔ y = − 4 x − 5 2 và d’: 2x – y = −1 ⇔ y = 2x + 1
Xét phương trình hoành độ giao điểm của d và d’:
− 4 x − 5 2 = 2 x + 1 ⇔ −4x – 5 = 4x + 2 ⇔ 8x = −7 ⇔ x = − 7 8
⇒ y = 2 x + 1 = 2. − 7 8 + 1 = − 3 4
Vậy tọa độ giao điểm của d và d’ là − 7 8 ; − 3 4
Suy ra nghiệm của hệ phương trình 4 x + 2 y = − 5 2 x − y = − 1 là x 0 ; y 0 = − 7 8 ; − 3 4
Từ đó x 0. y 0 = − 7 8 . − 3 4 = 21 32
Đáp án: A