
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔABC có
O là trung điểm của AB
H là trung điểm của BC
Do đó: OH là đường trung bình của ΔABC
Suy ra: OH//AC
hay OH\(\perp\)CB
Suy ra: ΔOHB vuông tại H

a: \(P=a+b=6\)
b: \(Q=a\cdot b=4\)
c: \(S=a^2+b^2=6^2-2\cdot4=36-8=28\)

\(a,\) Ta có \(OA=OB=OC=R=\dfrac{1}{2}AB\Rightarrow\Delta ABC\perp C\)
\(b,CB=\sqrt{AB^2-AC^2}=\sqrt{\left(AO+OB\right)^2-AC^2}\\ =\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
Ta có \(CA=R=CO\Rightarrow\Delta ACO\) đều
\(\Rightarrow\widehat{CAO}=\widehat{ACO}=\widehat{COA}=60\)
\(\Rightarrow\widehat{ABC}=90-\widehat{CAO}=90-60=30\)
và \(\widehat{ACB}=90\left(\Delta ABC\perp C\right)\)
\(c,\) Áp dụng HTL tam giác ABC vuông tại C có đường cao CH:
\(CH\cdot AB=AC\cdot AB\Leftrightarrow CH\cdot20=10\cdot10\sqrt{3}\\ \Leftrightarrow CH=\dfrac{100\sqrt{3}}{20}=5\sqrt{3}\left(cm\right)\)

có:
\(\sqrt{n+1}-\sqrt{n}\)
\(=\dfrac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\sqrt{n+1}+\sqrt{n}}\)
\(=\dfrac{n+1-n}{\sqrt{n+1}+\sqrt{n}}=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
Vì \(2\sqrt{n}< \sqrt{n+1}+\sqrt{n}< 2\sqrt{n+1}\)
\(\Rightarrow\dfrac{1}{2\sqrt{n}}>\dfrac{1}{\sqrt{n+1}+\sqrt{n}}>\dfrac{1}{2\sqrt{n+1}}\)
Vậy: \(\dfrac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \dfrac{1}{2\sqrt{n}}\)

Bài 4:
ĐKXĐ: \(x\ge3\)
Ta có: \(\sqrt{x^2-9}-\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)

a: Thay \(x=6-2\sqrt{5}\) vào A, ta được:
\(A=\dfrac{1-\sqrt{5}+1}{\sqrt{5}-1+1}=\dfrac{2-\sqrt{5}}{\sqrt{5}}=\dfrac{2\sqrt{5}-5}{5}\)
b: Ta có: \(B=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}+1}\)

Min của biểu thức này không tồn tại (nó chỉ tồn tại khi tam giác ABC là 1 tam giác suy biến nghĩa là 1 cạnh bằng 0)

a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)


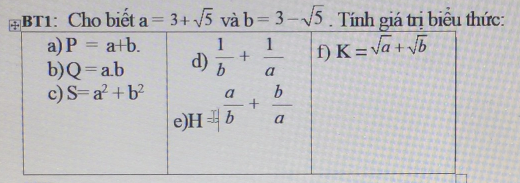

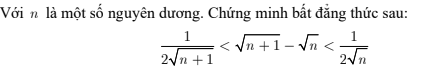 các bạn giúp mình đc ko ạ
các bạn giúp mình đc ko ạ 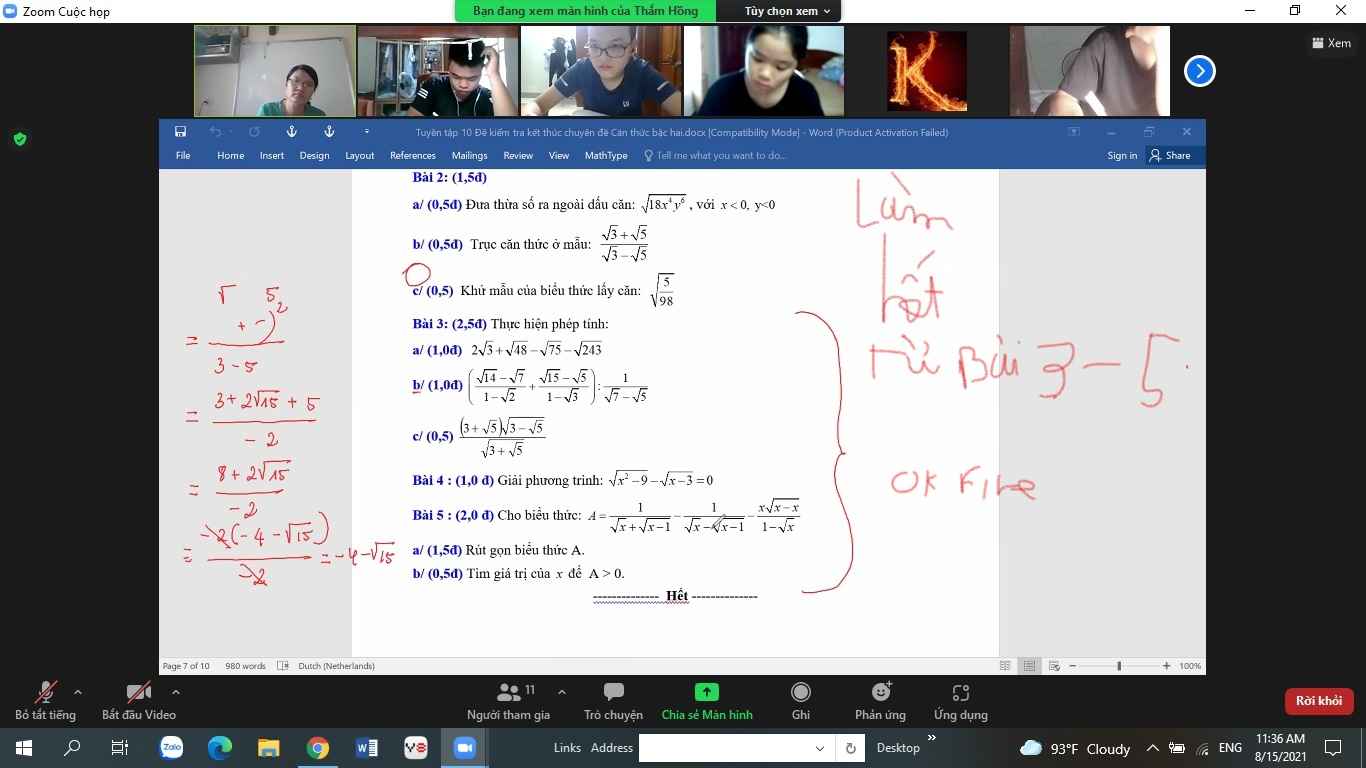
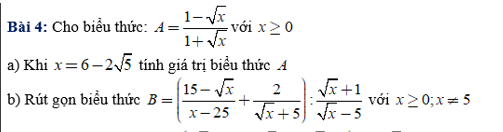
a) \(Q=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{3\sqrt{x}-x}{x+4\sqrt{x}+4}\left(đk:x\ge0,x\ne4\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{3\sqrt{x}-x}\)
\(=\dfrac{\left(x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(3\sqrt{x}-x\right)}\)
\(=\dfrac{\left(-x+2\sqrt{x}\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(3\sqrt{x}-x\right)}=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{-\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b) \(Q=2\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=2\Leftrightarrow2\sqrt{x}-6=\sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}=8\Leftrightarrow x=64\)
c) \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}-3< 0\end{matrix}\right.\)(do \(\sqrt{x}+2>\sqrt{x}-3\))
\(\Leftrightarrow-2< \sqrt{x}< 3\)
\(\Leftrightarrow0\le x< 9\) và \(x\ne4\)
a: Ta có: \(Q=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{3\sqrt{x}-x}{x+4\sqrt{x}+4}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{-\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{-\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Để Q=2 thì \(\sqrt{x}+2=2\sqrt{x}-6\)
\(\Leftrightarrow\sqrt{x}=8\)
hay x=64