
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔABC có
O là trung điểm của AB
H là trung điểm của BC
Do đó: OH là đường trung bình của ΔABC
Suy ra: OH//AC
hay OH\(\perp\)CB
Suy ra: ΔOHB vuông tại H

a: \(P=a+b=6\)
b: \(Q=a\cdot b=4\)
c: \(S=a^2+b^2=6^2-2\cdot4=36-8=28\)

a) \(Q=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{3\sqrt{x}-x}{x+4\sqrt{x}+4}\left(đk:x\ge0,x\ne4\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{3\sqrt{x}-x}\)
\(=\dfrac{\left(x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(3\sqrt{x}-x\right)}\)
\(=\dfrac{\left(-x+2\sqrt{x}\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(3\sqrt{x}-x\right)}=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{-\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b) \(Q=2\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=2\Leftrightarrow2\sqrt{x}-6=\sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}=8\Leftrightarrow x=64\)
c) \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}-3< 0\end{matrix}\right.\)(do \(\sqrt{x}+2>\sqrt{x}-3\))
\(\Leftrightarrow-2< \sqrt{x}< 3\)
\(\Leftrightarrow0\le x< 9\) và \(x\ne4\)
a: Ta có: \(Q=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{3\sqrt{x}-x}{x+4\sqrt{x}+4}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{-\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{-\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Để Q=2 thì \(\sqrt{x}+2=2\sqrt{x}-6\)
\(\Leftrightarrow\sqrt{x}=8\)
hay x=64

\(PT\Leftrightarrow9x^2+16x+96=9x^2+256y^2+576-96xy+768y-144x.\)
\(\Leftrightarrow256y^2-160x-96xy+768y+480=0\)
\(\Leftrightarrow8y^2-5x-3xy+24y+15=0\)
Đến chỗ này phân tích kiểu j được nhỉ

Bài nào bạn?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????

Đkxđ: \(\hept{\begin{cases}x\ge-\frac{1}{4}\\y\ge2\end{cases}}\)
\(\Leftrightarrow2+\sqrt{\left(\sqrt{x+\frac{1}{4}}+\frac{1}{2}\right)^2}=y\Leftrightarrow2+\frac{1}{2}+\sqrt{x+\frac{1}{2}}=y\Leftrightarrow\sqrt{x+\frac{1}{2}}+\frac{5}{2}=y\)
do x,y nguyên dương nên \(\sqrt{x+\frac{1}{2}}+\frac{5}{2}\)nguyên dương\(\Leftrightarrow\sqrt{x+\frac{1}{2}}=\frac{k}{2}\)(K là số nguyên lẻ, \(k>1\))
\(\Rightarrow x=\frac{k^2-2}{4}\)
do \(k^2\)là số chính phương chia 4 dư 0,1 \(\Rightarrow x=\frac{k^2-2}{4}\notin Z\)
=> ko tồn tại cặp số nguyên dương x,y tmđkđb

a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
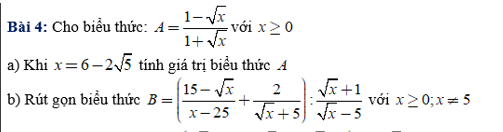

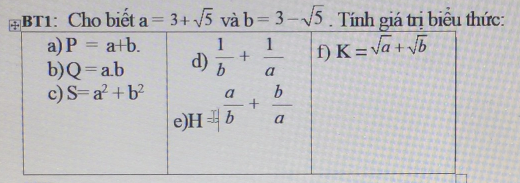



a: Thay \(x=6-2\sqrt{5}\) vào A, ta được:
\(A=\dfrac{1-\sqrt{5}+1}{\sqrt{5}-1+1}=\dfrac{2-\sqrt{5}}{\sqrt{5}}=\dfrac{2\sqrt{5}-5}{5}\)
b: Ta có: \(B=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}+1}\)