
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(\dfrac{2}{3}\sqrt{81}-\dfrac{1}{2}\sqrt{16}=\dfrac{2}{3}.9-\dfrac{1}{2}.4=6+2=8\)
b)\(0,5\sqrt{0,04}+5\sqrt{0,36}=0,5.0,2+5.0,6=0,1+3=3,1\)
c)\(\sqrt{\left(\sqrt{5}-3\right)^2}+\sqrt{\left(\sqrt{5}-13\right)^2}=\sqrt{5}-3+\sqrt{5}-13=2\sqrt{5}-16\)
Câu a em nhầm dấu - thành + ở cuối. Kết quả đúng là 6-2=4


1) ĐKXĐ: \(x\ge-5\)
\(pt\Leftrightarrow x+5=9\Leftrightarrow x=9-5=4\left(tm\right)\)
2) ĐKXĐ: \(x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\sqrt{x-3}=6\)
\(\Leftrightarrow2\sqrt{x-3}=6\Leftrightarrow\sqrt{x-3}=3\)
\(\Leftrightarrow x-3=9\Leftrightarrow x=12\left(tm\right)\)
3) ĐKXĐ: \(x\ge-1\)
\(pt\Leftrightarrow\sqrt{\left(x+1\right)^2}-2\sqrt{x+1}=0\)
\(\Leftrightarrow x+1-2\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{x+1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+1=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)


b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot NP=MN^2\left(1\right)\)
Xét ΔMNK vuông tại M có MQ là đường cao
nên \(NQ\cdot NK=MN^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot NP=NQ\cdot NK\)

c) C = \(\dfrac{4}{\sqrt{3}+1} - \dfrac{5}{\sqrt{3}-2} + \dfrac{6}{\sqrt{3}-3}\)
⇔ C = \(\dfrac{4(\sqrt{3}-1)}{2} - \dfrac{5(\sqrt{3}-2)}{-1} - \dfrac{6(\sqrt{3}+3)}{-6}\)
⇔ C = \(2\sqrt{3} -2 + 5\sqrt{3} + 10 - \sqrt{3} - 3\)
⇔ C = \(6\sqrt{3} + 5\)

3.
a, \(\sqrt{18x}=3\sqrt{2x}\)
b, \(\sqrt{75x^2y}=5\left|x\right|\sqrt{3y}\)
c, \(11\left|xy\right|\sqrt{5x}\)

a) \(Q=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{3\sqrt{x}-x}{x+4\sqrt{x}+4}\left(đk:x\ge0,x\ne4\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{3\sqrt{x}-x}\)
\(=\dfrac{\left(x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(3\sqrt{x}-x\right)}\)
\(=\dfrac{\left(-x+2\sqrt{x}\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(3\sqrt{x}-x\right)}=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{-\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b) \(Q=2\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=2\Leftrightarrow2\sqrt{x}-6=\sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}=8\Leftrightarrow x=64\)
c) \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}-3< 0\end{matrix}\right.\)(do \(\sqrt{x}+2>\sqrt{x}-3\))
\(\Leftrightarrow-2< \sqrt{x}< 3\)
\(\Leftrightarrow0\le x< 9\) và \(x\ne4\)
a: Ta có: \(Q=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{3\sqrt{x}-x}{x+4\sqrt{x}+4}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{-\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{-\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Để Q=2 thì \(\sqrt{x}+2=2\sqrt{x}-6\)
\(\Leftrightarrow\sqrt{x}=8\)
hay x=64
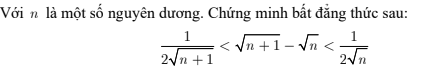 các bạn giúp mình đc ko ạ
các bạn giúp mình đc ko ạ 




có:
\(\sqrt{n+1}-\sqrt{n}\)
\(=\dfrac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\sqrt{n+1}+\sqrt{n}}\)
\(=\dfrac{n+1-n}{\sqrt{n+1}+\sqrt{n}}=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
Vì \(2\sqrt{n}< \sqrt{n+1}+\sqrt{n}< 2\sqrt{n+1}\)
\(\Rightarrow\dfrac{1}{2\sqrt{n}}>\dfrac{1}{\sqrt{n+1}+\sqrt{n}}>\dfrac{1}{2\sqrt{n+1}}\)
Vậy: \(\dfrac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \dfrac{1}{2\sqrt{n}}\)