
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn học lớp mấy rồi mà ko biết làm toán lớp mẫu giáo thế ?😁 ☺️ ☹️

Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
ti le 3 canh la 3/4/5 (dinh li pytago)
2 canh goc vuong lan luot la
125 : 5 x 4 = 100
125 : 5 x 3 = 75

x^2 + x - 2 = 0
<=> ( x^2 - x ) + ( 2x - 2 ) = 0
<=> x . ( x - 1 ) + 2 . ( x - 1 ) = 0
<=> ( x - 1 ) . ( x + 2 ) = 0
<=> x - 1 = 0 hoặc x + 2 = 0
<=> x = 1 hoặc x = -2
Vậy .......
Tk mk nha

a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E

Chu vi của bánh xe là:
70 x 3,14 = 219,8 (cm)
Khoảng cách từ nhà AN đến trường là:
984 x 219,8 = 216283,2 cm
Đáp số:...

Đây nè :
y=x^3+3x^2+1=(x+1)^3-3x <=>
y-3=(x+1)^3-3x-3 hay
y-3 = (x+1)^3 - 3(x+1) (*)
Nhìn vào (*) ta thấy rằng nếu chọn hệ trục tọa độ mới IXY với gốc tọa độ tại I(-1;3)
Khi đó X=x+1, Y=y-3 và hàm số trở thành Y=X^3 - 3X là hàm lẻ, đồ thị của nó (cũng chính là đồ thị hàm đã cho trong hệ tọa độ cũ) nhận I là tâm đối xứng.
Vậy tâm đối xứng của đồ thị hs đã cho là I(-1;3)
Nếu bạn đã học khảo sát hàm số bằng đạo hàm thì có cách này đơn giản hơn nhiều :
y'=3x^2+6x (nghiệm của y'=0 là hoành độ các cực trị, nhưng ta không quan tâm)
y''=6x+6 (nghiệm của y''=0 chính là hoành độ điểm uốn, cũng là tâm đối xứng)
y''=6x+6=0=>x= -1=>y=3

Gọi thời gian làm riêng của 2 người làm xong công việc lần lượt a ; b ( a;b > 0 )
1 giờ người thứ nhất làm được 1/a công việc
1 giờ người thứ 2 làm được 1/b công việc
Theo bài ra ta có hệ phương trình \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{6}{x}+\dfrac{3}{y}=\dfrac{2}{3}\end{matrix}\right.\)Đặt 1/x = u ; 1/y = v
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=\dfrac{5}{36}\\6u+3v=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{1}{12}\\v=\dfrac{1}{18}\end{matrix}\right.\)Theo cách đặ x = 12 ; y = 18
Vậy ...

PT : \(\sqrt{x^3-5}-\sqrt[3]{x^3+8}=1\) ( ĐKXĐ : \(x\ge\sqrt[3]{5}\))
\(\Leftrightarrow x^3+8=\left(\sqrt{x^3-5}-1\right)^3\)
\(\Leftrightarrow x^3+8=\left(\sqrt{x^3-5}\right)^3-3.\left(x^3-5\right)+3\sqrt{x^3-5}-1\)
\(\Leftrightarrow\left(\sqrt{x^3-5}\right)^3-4\left(x^3-5\right)+3\sqrt{x^3-5}-14=0\)
Đặt \(y=\sqrt{x^3-5},y\ge0\), pt trở thành \(y^3-4y^2+3y-14=0\)
Tới đây bạn tự giải !
\(a=\sqrt{x^3-5};\text{ }b=\sqrt[3]{x^3+8}\)
\(\Rightarrow\hept{\begin{cases}a-b=1\\b^3-a^2=x^3+8-\left(x^3-5\right)=13\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=b+1\\b^3-\left(b+1\right)^2=13\text{ (1)}\end{cases}}\)
\(\left(1\right)\Leftrightarrow b^3-b^2-2b-14=0\)
Nghiệm xấu rồi.

Ta có: \(1+\left(\dfrac{2a+\sqrt{a}-1}{1-a}-\dfrac{2a\sqrt{a}-\sqrt{a}+a}{1-a\sqrt{a}}\right)\cdot\dfrac{a-\sqrt{a}}{2\sqrt{a}-1}\)
\(=1+\left(\dfrac{-2\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}\right)\cdot\dfrac{a-\sqrt{a}}{2\sqrt{a}-1}\)
\(=1+\left(\dfrac{-\left(2\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)+\sqrt{a}\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{2\sqrt{a}-1}\)
\(=1+\dfrac{\left(2\sqrt{a}-1\right)\left(-a-\sqrt{a}-1+a+\sqrt{a}\right)}{a+\sqrt{a}+1}\cdot\dfrac{\sqrt{a}}{2\sqrt{a}-1}\)
\(=1+\dfrac{-\sqrt{a}}{a+\sqrt{a}+1}\)
\(=\dfrac{a+\sqrt{a}+1-\sqrt{a}}{a+\sqrt{a}+1}\)
\(=\dfrac{a+1}{a+\sqrt{a}+1}\)

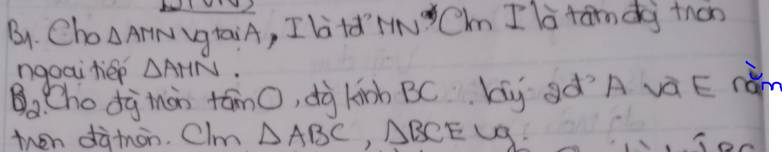
a, Với \(x\ge0;x\ne1\)
\(A=\frac{\sqrt{x}+1}{\sqrt{x}-1}-\frac{\sqrt{x}-1}{\sqrt{x}+1}-\frac{4}{x-1}\)
\(=\frac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{x-1}-\frac{4}{x-1}=\frac{4\sqrt{x}-4}{x-1}=\frac{4}{\sqrt{x}+1}\)
b, Ta có : \(A=\frac{1}{2}\Rightarrow\frac{4}{\sqrt{x}+1}=\frac{1}{2}=\frac{4}{8}\Rightarrow\sqrt{x}+1=8\Leftrightarrow\sqrt{x}=7\Leftrightarrow x=49\)
Vậy x = 49 thì A = 1/2
c, Ta có : \(x=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}=\sqrt{3}+1-\sqrt{3}+1=2\)
Thay vào biểu thức A ta được : \(A=\frac{4}{\sqrt{2}+1}=4\left(\sqrt{2}-1\right)\)
d, Để x thuộc Z khi \(\sqrt{x}+1\) là ước của 4 = { \(\pm1;\pm2;\pm4\)}
TH1 : Thay x = 0 vào biểu thức A ta được : \(\frac{4}{\sqrt{x}+1}\Rightarrow\frac{4}{0+1}=4\)* đúng *
Vì giá trị A là số tự nhiên
TH2 : Thay x = 1 vào biểu thức A ta được : \(\frac{4}{2}=2\)* đúng *
Vì giá trị A là số tự nhiên
TH3 : Thay x = 9 vào biểu thức A ta được : \(\frac{4}{3+1}=1\)* đúng *
Vì giá trị A là số tự nhiên
Ps : tương tự với bài 2 nhé
A=\(\frac{4}{\sqrt{x}+1}\)