Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thức tính số hạt nhân còn lại tại thời điểm t:

Đáp án C

Đáp án: A.
Tại thời điểm t1: số hạt nhân còn lại N = N0/5 ⇒ 2t1/T = 5
Tại thời điểm t2: số hạt nhân còn lại N = N0/20 ⇒ 2(t1+ 100)/T = 20 ⇒ 5.2100/T = 20
⇒ T = 100/2 = 50s.

Sau thời gian t1 số hạt nhân còn lại là
\(N = N_0 2^{-\frac{t}{T}}\)=> \(\frac{N}{N_0}= 0,2= 2^{-\frac{t_1}{T}}=> t_1 = -T.\ln_20,2.\)
Sau thời điểm t2 thì số hạt nhân còn lại là
\(N_1 = N_0 2^{-\frac{t_2}{T}}=> \frac{N}{N_0} = 0,05 = 2^{-\frac{t_2}{T}}\)=> \(t_2 = -T\ln_20,05.\)
Mà \(t_2 = t_1 +100\)
=> \(-T \ln_2 0,05 = -T\ln_2 0,2 + 100\)
=> \(T = \frac{100}{\ln_2{(0,2/0,05)}}=50 s. \)

Ở thời điểm t 1 : người ta thấy có 60% số hạt nhân của mẫu bị phân rã thành chất khác nên số hạt nhân còn lại là:
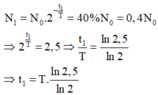
Ở thời điểm t 2 : trong mẫu chỉ còn lại 5% số hạt nhân phóng xạ nên:
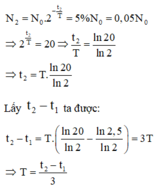
Đáp án C

t1 có 80% chất bị phân rã tức là còn lại 20 %+> \(m\left(t_1\right)=0.2m_0=m_0.2^{-\frac{t_1}{T}}.\)
t2 = t1+100s số hạt nhân còn lại là \(m\left(t_2\right)=0.05m_0=m_0.2^{-\frac{t_2}{T}}.\)
Chia hai phương trình cho nhau ta được
\(\frac{0.2}{0.05}=2^{\frac{\left(t_2-t_1\right)}{T}}\)
=> \(\frac{t_2-t_1}{T}=2\Rightarrow100s=2T\Rightarrow T=50s.\)
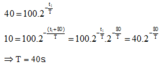
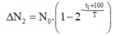
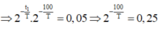
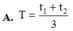
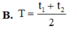
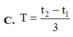
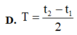
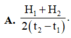
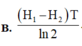
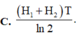
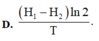

Đáp án A