Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

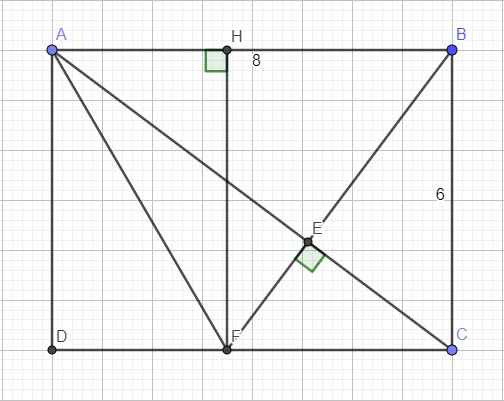
Áp dụng định lý Pitago cho tam giác vuông ABC
\(AC=\sqrt{AB^2+BC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC với đường cao BE:
\(AB^2=AE.AC\Rightarrow AE=\dfrac{AB^2}{AC}=6,4\left(cm\right)\)
\(AB.AC=BE.AC\Rightarrow AE=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b.
Ta có: \(EC=AC-AE=3,6\left(cm\right)\)
Do AB song song CF, theo định lý Talet:
\(\dfrac{CF}{AB}=\dfrac{CE}{AE}\Rightarrow CF=\dfrac{AB.CE}{AE}=4,5\left(cm\right)\)
\(\Rightarrow DF=DC-CF=8-4,5=3,5\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADF:
\(AF=\sqrt{AD^2+DF^2}=\dfrac{\sqrt{193}}{2}\left(cm\right)\)
Pitago tam giác vuông BCF:
\(BF=\sqrt{BC^2+CF^2}=7,5\left(cm\right)\)
Kẻ FH vuông góc AB \(\Rightarrow ADFH\) là hình chữ nhật (tứ giác 3 góc vuông)
\(\Rightarrow FH=AD=6\left(cm\right)\)
\(S_{ABF}=\dfrac{1}{2}FH.AB=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)

a) Hình tròn có bán kính 2cm có diện tích : S = π. 2 2 = 4π ( c m 2 )
b) Hình vuông có độ dài cạnh 3,5cm có diện tích : S = 3 , 5 2 = 12,25 ( c m 2 )
c) tam giác có các cạnh 3cm,4cm,5cm nên nó là tam giác vuông
Khi đó tam giác có diện tích: S =(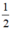 ).3.4 =6(
c
m
2
)
).3.4 =6(
c
m
2
)
d) Nửa mặt cầu bán kính 4cm có diện tích : S= (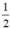 ).4.
π
.
4
2
= 32
π
(
c
m
2
)
).4.
π
.
4
2
= 32
π
(
c
m
2
)
Vậy trong các hình trên thì nửa mặt cầu bán kính 4cm có diện tích lớn nhất
Vậy chọn đáp án (D)
S(ACF) = S(ACFG) -S(AFG)
S(ACFG) = S(ACD) + S(CDGF) = \(\frac{8.8}{2}\)+ \(\frac{\left(8+4\right).4}{2}\)= 32 + 24 = 56 (cm2) (1)
S(AFG) = \(\frac{\left(AD+DG\right).GF}{2}\)= \(\frac{\left(8+4\right).4}{2}\)= 24 cm2 (2)
vậy từ (1) và (2) --> S(ACF) = 56 - 24 = 32 cm2