Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toàn bộ nghiệm của 3 pt này đều là nghiệm thực, không có nghiệm phức nào
a. \(x^2-3x-2=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{17}}{2}\\x=\dfrac{3-\sqrt{17}}{2}\end{matrix}\right.\)
b. \(x^4-5x^2+6=0\Rightarrow\left[{}\begin{matrix}x^2=2\\x^2=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x=\pm\sqrt{3}\end{matrix}\right.\)
c. \(-x^2+4x+5=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)


Điều kiện x>0. Nhận thấy x=2 là nghiệm.
Nếu x>2 thì
\(\frac{x}{2}>\frac{x+2}{4}>1\); \(\frac{x+1}{3}>\frac{x+3}{5}>1\)
Suy ra
\(\log_2\frac{x}{2}>\log_2\frac{x+2}{4}>\log_4\frac{x+2}{4}\)hay :\(\log_2x>\log_2\left(x+2\right)\)
\(\log_3\frac{x+1}{3}>\log_3\frac{x+3}{5}>\log_5\frac{x+3}{5}\) hay \(\log_3\left(x+1\right)>\log_5\left(x+3\right)\)
Suy ra vế trái < vế phải, phương trình vô nghiệm.
Đáp số x=2

b) Ta có: \(x^2-4x+20=0\)
\(\Leftrightarrow x^2-4x+4+16=0\)
\(\Leftrightarrow\left(x-2\right)^2+16=0\)(Vô lý)
Vậy: \(S=\varnothing\)
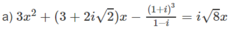
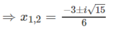
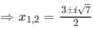

Bạn coi lại đề câu a, chỗ \(\log_5-x\) đó
b.
\(\Leftrightarrow9^x-3^x-2.3^x-2=0\)
\(\Leftrightarrow3^x\left(3^x-1\right)-2\left(3^x-1\right)=0\)
\(\Leftrightarrow\left(3^x-2\right)\left(3^x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3^x=2\\3^x=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\log_32\\x=0\end{matrix}\right.\)