
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
Số đo các góc còn lại là \(47^0;133^0;133^0\)

Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)


Bài 8:
a) \(\left(-3,5\right):\left(-2\dfrac{3}{5}\right)=\dfrac{7}{2}:\dfrac{13}{2}=\dfrac{7}{2}\cdot\dfrac{2}{13}=\dfrac{7\cdot2}{2\cdot13}=\dfrac{7}{13}\)
b) \(\left(-\dfrac{11}{15}\right):1\dfrac{1}{10}=\left(-\dfrac{11}{15}\right):\dfrac{11}{10}=\left(-\dfrac{11}{15}\right)\cdot\dfrac{10}{11}=\dfrac{-11\cdot10}{15\cdot11}=-\dfrac{10}{15}=-\dfrac{2}{3}\)
c) \(2\dfrac{2}{3}:\left(-3\dfrac{3}{4}\right)=\dfrac{8}{3}:-\dfrac{15}{4}=\dfrac{8}{3}\cdot-\dfrac{4}{15}=\dfrac{8\cdot4}{3\cdot15}=-\dfrac{32}{45}\)
Bài 7:
a) \(\left(-\dfrac{3}{25}\right):6=\left(-\dfrac{3}{25}\right)\cdot\dfrac{1}{6}=\dfrac{-3\cdot1}{25\cdot6}=-\dfrac{1}{50}\)
b) \(-\dfrac{5}{23}:-2=\dfrac{5}{23}\cdot\dfrac{1}{2}=\dfrac{5\cdot1}{23\cdot2}=\dfrac{5}{26}\)
c) \(\dfrac{-7}{11}:-3,5=\dfrac{7}{11}:\dfrac{7}{2}=\dfrac{7}{11}\cdot\dfrac{2}{7}=\dfrac{7\cdot2}{11\cdot7}=\dfrac{2}{11}\)

a) \(2^4+8\left[\left(-2\right)^2:\dfrac{1}{2}\right]^0-2^{-2}.4+\left(-2\right)^2\)
\(=2^4+8.1-\dfrac{1}{4}.4+4\)
\(=16+8-1+4\)
\(=24-1+4\)
\(=23+4\)
\(=27\)







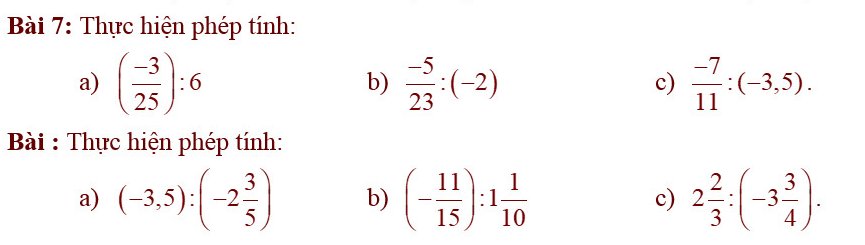


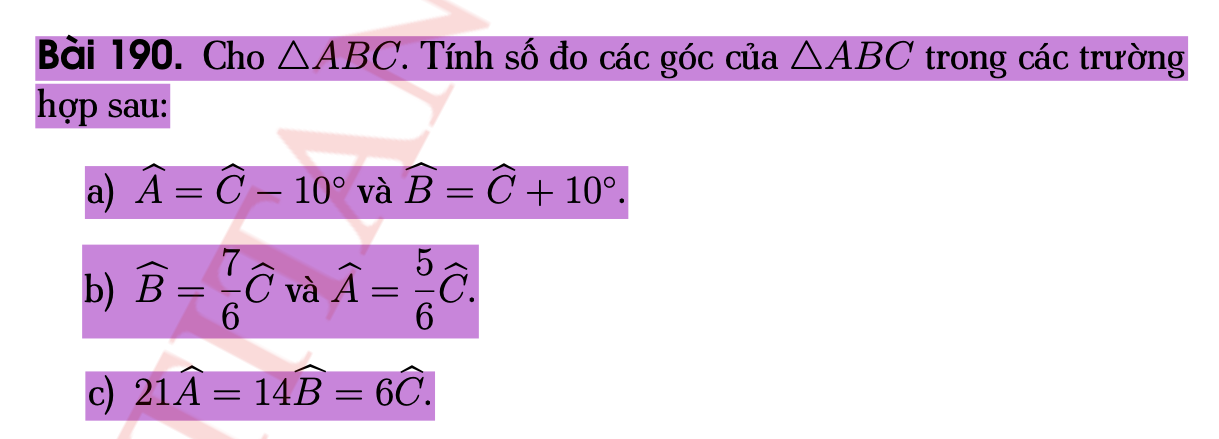
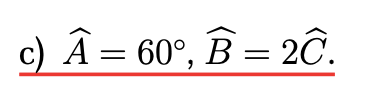
\(\frac{kA}{c}=\frac{k}{a_1.a_2}+\frac{k}{a_2.a_3}+\frac{k}{a_3.a_4}+...+\frac{k}{a_{n-1}.a_n}=\)
\(=\frac{a_2-a_1}{a_1.a_2}+\frac{a_3-a_2}{a_{2.}.a_3}+\frac{a_4-a_3}{a_3.a_4}+..+\frac{a_n-a_{n-1}}{a_{n-1}.a_n}=\)
\(=\frac{1}{a_1}-\frac{1}{a_2}+\frac{1}{a_2}-\frac{1}{a_3}+\frac{1}{a_3}-\frac{1}{a_4}+...+\frac{1}{a_{n-1}}-\frac{1}{a_n}=\)
\(=\frac{1}{a_1}-\frac{1}{a_n}=\frac{a_n-a_1}{a_1.a_n}\Rightarrow A=\frac{\left(a_n-a_1\right).c}{a_1.a_n.k}\)