Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Xét tam giác vuông HMO có
^HOM=30 độ (Oz là phân giác ^xOy)
=> MH=OM/2 (trong tam giác vuông cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)
+ Xét tam giác vuông KNO chứng minh tương tự ta cùng có NK=ON/2
=> MH+NK=(OM+ON)/2 => OM+ON=2(MH+NK)

b) Xét ΔOMH vuông tại M và ΔONK vuông tại N có
OM=ON(gt)
\(\widehat{O}\) chung
Do đó: ΔOMH=ΔONK(cạnh góc vuông-góc nhọn kề)
Suy ra: OH=OK(hai cạnh tương ứng) và \(\widehat{H}=\widehat{K}\)(hai góc tương ứng)
Ta có: ON+NH=OH(N nằm giữa O và H)
OM+MK=OK(M nằm giữa O và K)
mà ON=OM(gt)
và OH=OK(cmt)
nên NH=MK
Xét ΔINH vuông tại N và ΔIMK vuông tại M có
NH=MK(cmt)
\(\widehat{H}=\widehat{K}\)(cmt)
Do đó: ΔINH=ΔIMK(cạnh góc vuông-góc nhọn kề)
Suy ra: IN=IM(hai cạnh tương ứng)
Xét ΔMIN có IN=IM(cmt)
nên ΔMIN cân tại I(Định nghĩa tam giác cân)
c) Ta có: ΔIMK vuông tại M(gt)
nên IK là cạnh huyền
Suy ra: IK là cạnh lớn nhất trong ΔIMK(Định lí)
hay IK>IM
mà IM=IN(cmt)
nên IK>IN

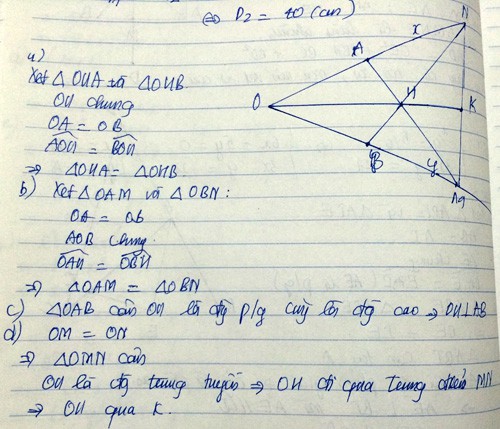
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOM}\) chung
Do đó: ΔOAM=ΔOBN
Suy ra OM=ON
b: Xét ΔBHM vuông tại B và ΔAHN vuông tại A có
BM=AN
\(\widehat{BHM}=\widehat{AHN}\)
Do đó: ΔBHM=ΔAHN
Suy ra: HN=HM
mà OM=ON
và IM=IN
nên O,H,I thẳng hàng

+) Xét tg ONB và OMA có
OB= OA (gt)
Góc O chung
Góc B = góc A(=90)
=> ∆ OMA (ch - gn)
=> />+) Ta có OA + AN = ON
OB+ BM= OM
Mà OA= OB
/>=> AN = BM
+) XÉT ∆OAH và ∆ OBH
OH cạnh cchung
OA= OB
góc A = góc B
=>∆ OAH= ∆ OBH( cho CGV)
=> AOH= BOH
=> OH là phân giác xOy
ta có (cmt)
=> ∆ ONM cân tại O
OI là trung tuyến => OI là đường cao
OI vuông góc NM(1)
Ta có MA, NB lần lượt vuông góc với Ox, Oy
MA cắt NB tại H
=> H là trực tâm của ∆OMN
=> OH vuông góc NM(2)
từ (1)(2)=> O , H , I thẳng hàng ( qua O chỉ kẻ đc duy nhất 1 đường thẳng vuông góc NM)