Question

[Linh Lê]

Bài 4: Cho tam giác đều ABC, gọi D, E, F là trung điểm của AB, AC, BC. Chứng minh tam giác DEF là tam giác đều.

Answer 1

[Υσɾυshἱκα Υυɾἱ]

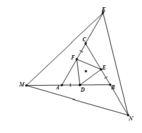
\(\Delta\)ABC là \(\Delta\)đều => AB=BC=CA mà D,E,F là trung điểm của AB,BC,CA=>AD=DB=BF=CF=CE=EA

xét \(\Delta\)ADE và \(\Delta\)BFD có:

AD=BF(cmt)

góc A=góc B(\(\Delta\)ABC là \(\Delta\)đều)

AE=BD(cmt)

=> \(\Delta\)ADE = \(\Delta\)BFD(c.g.c)(1)

xét \(\Delta\)BFD và\(\Delta\)CEF có:

BD=CE(cmt)

góc B=góc C(\(\Delta\)ABC là \(\Delta\)đều)

BF=CF(cmt)

=> \(\Delta\)ADE = \(\Delta\)BFD(c.g.c)(2)

từ(1) và(2)=> \(\Delta\)ADE = \(\Delta\)BFD= \(\Delta\)BFD=>DE=DF=FE=>\(\Delta\)DEF là \(\Delta\)đều

Answer 2

[Nguyễn Lê Phước Thịnh]

Xét ΔABC có 

D là trung điểm của AB(gt)

F là trung điểm của BC(gt)

Do đó: DF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)

Suy ra: DF//AC và \(DF=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)

Xét ΔABC có

F là trung điểm của BC(gt)

E là trung điểm của AC(gt)

Do đó: FE là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)Suy ra: FE//AB và \(FE=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)

Xét ΔABC có 

D là trung điểm của AB(gt)

E là trung điểm của AC(gt)

Do đó: DE là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)

Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(3)

Ta có: ΔABC đều(gt)

nên AB=AC=BC(4)

Từ (1), (2), (3) và (4) suy ra DE=EF=DF

Xét ΔDEF có DE=DF=EF(cmt)

nên ΔDEF đều(Định nghĩa tam giác đều)