Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔBMN và ΔCMA có
góc BMN=góc AMC
góc MNB=góc MAC
=>ΔBMN đồng dạng với ΔCMA

a: Xét ΔABC co AI là phân giác
nên IB/IC=AB/AC
=>AB/6=3/4,5=2/3
=>AB=4cm
Xét ΔBAC có MI//AC
nên MI/AC=BM/BA=BI/BC=3/7,5=2/5
=>MI/6=BM/4=2/5
=>MI=12/5cm; BM=8/5cm
b: MB/MA=BI/IC=BA/AC

a) Xét tam giác AHD và tam giác CKD có:
AHD=CKD=90
\(D_1=D_2\) (2 góc đối đỉnh)
=> tam giác AHD đồng dạng tam giác CKD (g-g)
=> đpcm
b) Xét tam giác AHB và tam giác CKB có
AHB=BKC=90
ABD=DBC ( BD là tia phân giác ABC)
=> Tam giác AHB đồng dạng CKB (g-g)
=> \(\dfrac{AB}{HB}=\dfrac{BC}{KB}=>AB.KB=BC.HB\)

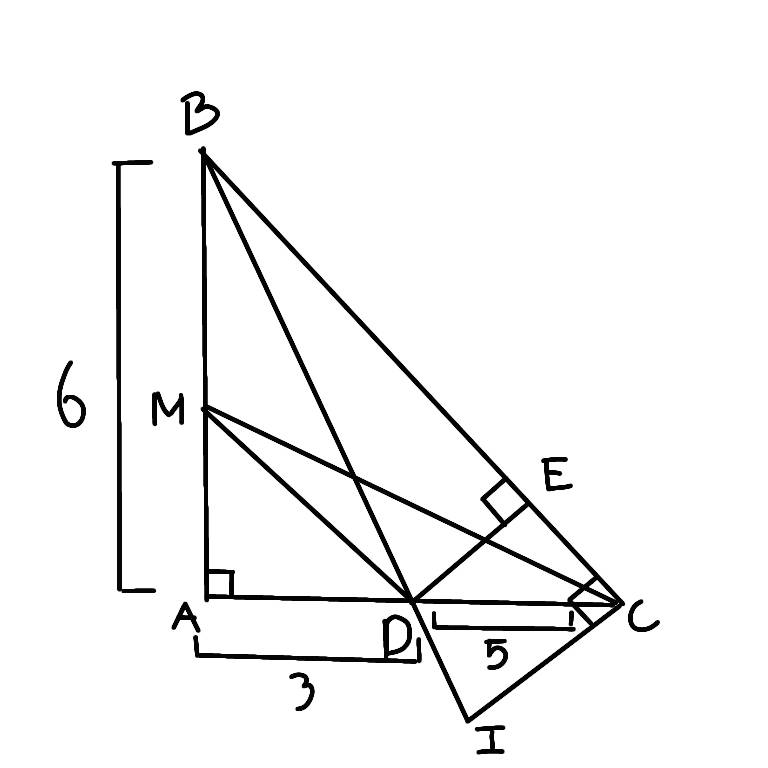 a. Tính BC
a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AH=9*12/15=7,2cm
b: ΔHAB vuông tại H có HM vuông góc AB
nên MH^2=MA*MB

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
MN//BC
Do đó: N là trung điểm của AC
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Bài 2:
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=12(cm)
b: Xét ΔABC có
MN//AC
nên \(\dfrac{MN}{AC}=\dfrac{BM}{AB}\)
hay MN=6(cm)

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
MN//BC
Do đó: N là trung điểm của AC
b: Xét ΔACB có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Bài 2:
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=12(cm)
b: Xét ΔABC có
M là trung điểm của AB
MN//AC
Do đó: N là trung điểm của BC
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: \(MN=\dfrac{AC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
a: ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>BC=20(cm)
Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{12}=\dfrac{CM}{20}\)
=>\(\dfrac{AM}{3}=\dfrac{CM}{5}\)
mà AM+CM=AC=16cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{16}{8}=2\)
=>\(AM=2\cdot3=6\left(cm\right);CM=5\cdot2=10\left(cm\right)\)
Xét ΔABC có MN//BC
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AC}\)
=>\(\dfrac{MN}{20}=\dfrac{6}{16}=\dfrac{3}{8}\)
=>\(MN=20\cdot\dfrac{3}{8}=\dfrac{60}{8}=7,5\left(cm\right)\)
b: Bạn ghi lại đề nha bạn