Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
b) Xét ΔDBI vuông tại I và ΔDCI vuông tại I có
DI chung
BI=CI(I là trung điểm của BC)
Do đó: ΔDBI=ΔDCI(hai cạnh góc vuông)
Suy ra: \(\widehat{DBI}=\widehat{DCI}\)(hai góc tương ứng)
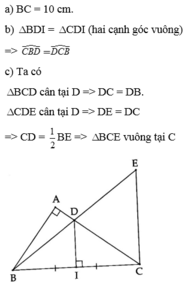
c) Xét ΔECB có
CD là đường trung tuyến ứng với cạnh EB
\(CD=\dfrac{EB}{2}\)
Do đó: ΔECB vuông tại C(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
Bài 4:
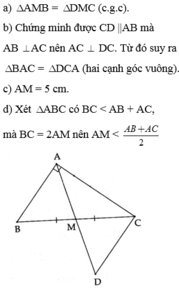
a) Ta có: \(AM=\dfrac{1}{2}BC\)(gt)
mà \(BM=CM=\dfrac{1}{2}BC\)(gt)
nên AM=BM=CM
Xét ΔABM có MA=MB(cmt)
nên ΔABM cân tại M
Suy ra: \(\widehat{AMB}=180^0-2\widehat{MAB}\)
\(\Leftrightarrow180^0-\widehat{CMA}=180^0-2\widehat{MAB}\)
hay \(\widehat{CMA}=2\cdot\widehat{MAB}\)
Xét ΔACM có MA=MC(cmt)
nên ΔACM cân tại M
Suy ra: \(\widehat{AMC}=180^0-2\cdot\widehat{MAC}\)
\(\Leftrightarrow180^0-\widehat{BMA}=180^0-2\cdot\widehat{MAC}\)
hay \(\widehat{BMA}=2\cdot\widehat{MAC}\)
b) Ta có: \(\widehat{BAC}=\widehat{MAB}+\widehat{MAC}\)
\(=\dfrac{1}{2}\left(\widehat{AMB}+\widehat{AMC}\right)\)
\(=\dfrac{1}{2}\cdot180^0=90^0\)

c/ Ta có tính chất: Trong 1 tam giác vuông, trung tuyến của góc vuông đến cạnh đối diện (cạnh huyền) sẽ bằng 1/2 cạnh huyền.
Xét tam giác vuông ABC, có trung tuyến AM, vậy AM=CM (=1/2 BC) => Tam giác ACM cân ( 2 cạnh bên bằng nhau) => ^ MCA=^MAC
Xét tam giác DMB và tam giác CMA
Có: CM=MB ( M trugn điểm)
DM=AM ( gt)
^DMB=^CMA (đđ)
Vậy hai tam giác =nhau =>^BDM=^MAC và ^DBM=^
B suy tiếp nhé!
Bạn tự vẽ hình nha!
Xét tam giác ABC vuông tại A, có: \(BC^2=AB^2+AC^2\)
\(225=81+AC^2\)
\(\Rightarrow AC^2=144\)
\(\Rightarrow AC=12\left(cm\right)\)
Xét tam giác MAB và tam giác MDC:
Có: DM=AM (gt)
CM=MB (AM trung tuyến)
Góc DMC=Góc AMB (đđ)
Vậy tam giác MAB= tam giác MDC (C.G.C)

a: \(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
b: XétΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
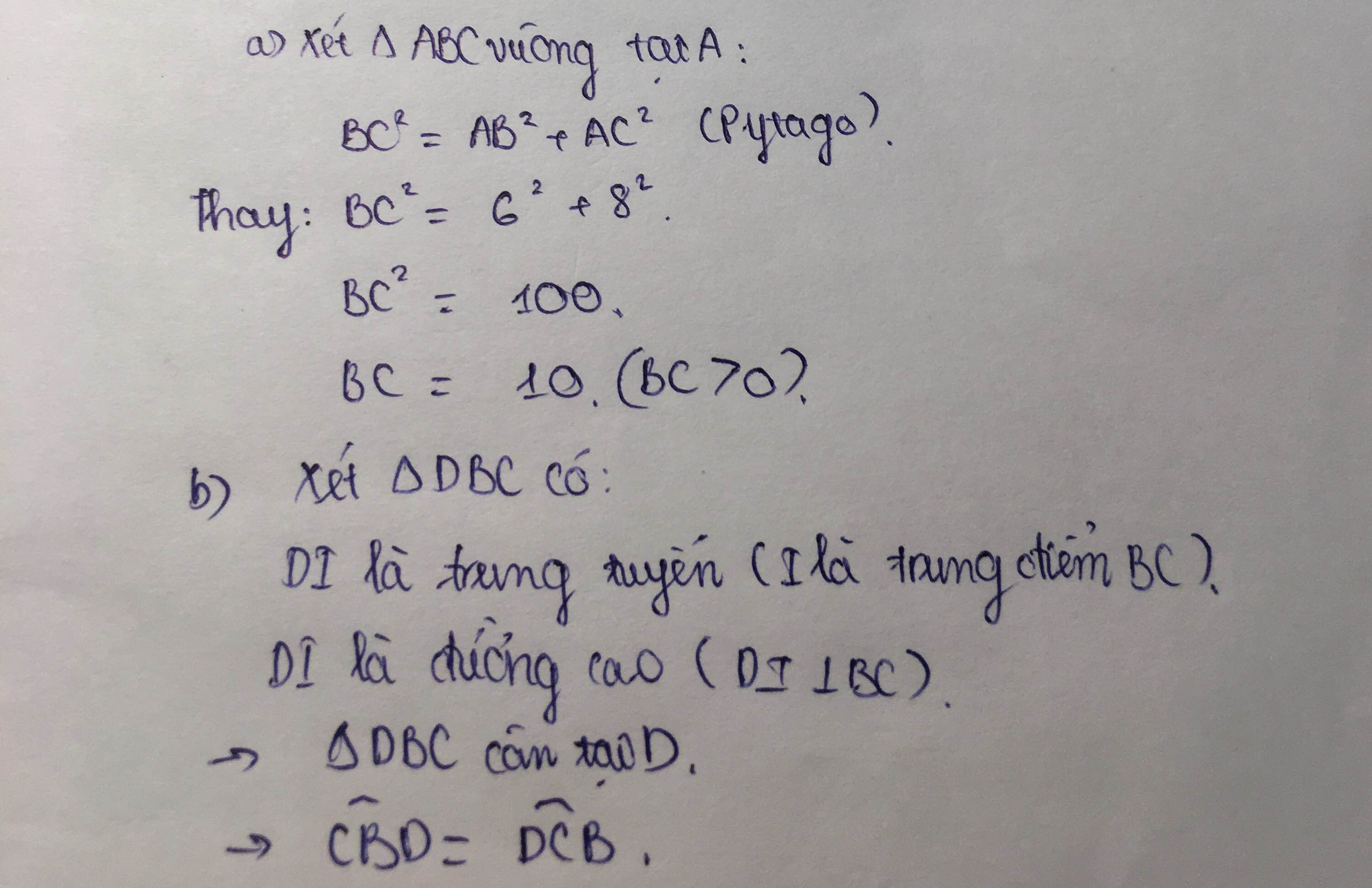

Bài 3:
a) Xét ΔAMC và ΔDMB có
MA=MD(gt)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB(gt)
Do đó: ΔAMC=ΔDMB(c-g-c)
Suy ra: \(\widehat{ACM}=\widehat{DBM}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//DB(Dấu hiệu nhận biết hai đường thẳng song song)
mà AC\(\perp\)AB(gt)
nên DB\(\perp\)AB
hay \(\widehat{ABD}=90^0\)
b) Xét ΔABD vuông tại B và ΔBAC vuông tại A có
BA chung
BD=AC(ΔDMB=ΔAMC)
Do đó: ΔABD=ΔBAC(hai cạnh góc vuông)
c) Ta có: ΔABD=ΔBAC(cmt)
nên AD=BC(hai cạnh tương ứng)
mà \(AM=\dfrac{1}{2}AD\)(gt)
nên \(AM=\dfrac{1}{2}BC\)