Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

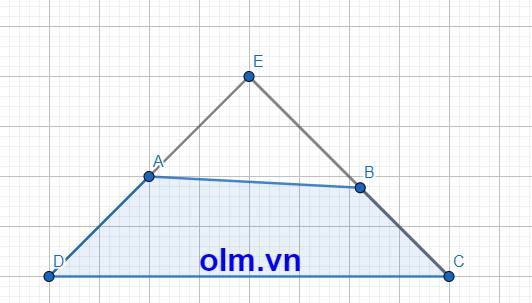
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)

Xét tam giác ABD có MN là đường trung bình => MN//=AD/2
Xét tam giác ACD có PQ là đường trung bình => PQ//=AD/2
=> MN//=PQ => Tứ giác MNPQ Là hình bình hành (1)
Tương tự ta cũng chứng minh được NP//=MQ//=BC/2
Ta có ^DAB+^AMN=180 (Hai góc trong cùng phía)
Ta có ^CBA+^BMQ=180 (lý do như trên)
=> (^DAB+^CBA)+(^AMN+^BMQ)=360 => ^AMN+^BMQ=360-^DAB+^CBA=360-270=90
Ta có ^AMB=^AMN+^BMQ+^NMQ=180=> ^NMQ=180-^AMN+^BMQ=180-90=90 (2)
Từ (1) và (2) => MNPQ là hình chữ nhật

Vì BD là phân giác của ABC và ADC
Xét ∆ADB ta có :
A + ABD + ADB = 180°
ABD + ADB = 180 - 85 = 95°
Mà 2ABD + 2ADB = 95°
=> ABC + ADC = 95 * 2 = 190°
Mà A + ABC + ADC + C = 360°
=> C = 360 - 85 - 190 = 85°

c,
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=gócBDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
+ AD=BC (*)
+ Góc ADB=góc BCA(**)
Từ (*) và (**) suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau )
cô làm rồi em ơi https://olm.vn/cau-hoi/bai-3-tu-giac-abcd-co-goc-c-goc-d-90-do-chung-minh-rang-ac2-bd-ab2cd2.8140260328277