KT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 7 2023
\(\left(1+\dfrac{2}{3}\right).\left(1+\dfrac{2}{4}\right).\left(1+\dfrac{2}{5}\right)....\left(1+\dfrac{2}{2020}\right).\left(1+\dfrac{2}{2021}\right)\)
= \(\dfrac{5}{3}.\dfrac{6}{4}.\dfrac{7}{5}.\dfrac{8}{6}.\dfrac{9}{7}....\dfrac{2022}{2020}.\dfrac{2023}{2021}\)
= \(\dfrac{1}{3}.\dfrac{1}{4}.2022.2023\)
= \(\dfrac{337.2023}{2}\)
= \(\dfrac{\text{681751}}{2}\)
BL
0
BL
1
KT
ÉT Ô ÉT
Câu 3: Tìm x biết:
|x + 1| + |x + 2| + |x + 2020| = 4x
Giúp mik với!!!
Mik hứa Tick cho… Pls
2
22 tháng 4 2023
TH1 : \(x< -2020\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) - ( x + 2020 ) = 4x
<=> -3x - 2023 = 4x <=> -7x = 2023 <=> x = -289
TH2 : \(-2020\le x< -2\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) + x + 2020 = 4x
<=> -x + 2017 = 4x
<=> -5x = -2017 <=> x = 2017/5 ( = 403,4 )
TH3 : \(-2\le x< -1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) + x + 2 + x + 2020 = 4x
<=> x + 2021 = 4x <=> -3x = -2021 <=> x = 2021/3
TH4 : \(x>-1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = x + 1 + x + 2 + x + 2020 = 4x
<=> 3x + 2023 = 4x
<=> -x = -2023 <=> x = 2023
Vậy...
22 tháng 4 2023
TH1: x ≥ 0
Khi đó \(\left|x+1\right|+\left|x+2\right|+\left|x+2020\right|=x+1+x+2+x+2020\)
\(=3x+2023=4x\)
Suy ra \(4x-3x=x=2023\) (thỏa mãn điều kiện)
TH2: x < 0
Khi đó 4x < 0 hay vế phải luôn là một số âm. Tuy nhiên vế trái luôn luôn có giá trị lớn hơn 0 nên luôn là 0 hoặc là một số dương, suy ra vô lí.
Tóm lại, x = 2023.
LC
9
PG
2
7 tháng 10 2020
Ta có: \(\left|x+\frac{1}{2021}\right|\ge0\) ; \(\left|x+\frac{2}{2021}\right|\ge0\) ; ... ; \(\left|x+\frac{2020}{2021}\right|\ge0\) \(\left(\forall x\right)\)
\(\Rightarrow\left|x+\frac{1}{2021}\right|+\left|x+\frac{2}{2021}\right|+...+\left|x+\frac{2020}{2021}\right|\ge0\left(\forall x\right)\)
\(\Rightarrow2021x\ge0\Rightarrow x\ge0\)
Từ đó ta được: \(x+\frac{1}{2021}+x+\frac{2}{2021}+...+x+\frac{2020}{2021}=2021x\)
\(\Leftrightarrow2020x+\frac{1+2+...+2020}{2021}=2021x\)
\(\Leftrightarrow x=\frac{\left(2020+1\right)\left[\left(2020-1\right)\div1+1\right]}{2021}\)
\(\Leftrightarrow x=\frac{2021\cdot2020}{2021}=2020\)
Vậy x = 2020
NC
11 tháng 3 2021
\(\left|\frac{x+1}{2021}\right|+\left|\frac{x+2}{2021}\right|+...+\left|\frac{x+2020}{2021}\right|=2021x\)
Ta có:\(\left|\frac{x+1}{2021}\right|\ge0;\left|\frac{x+2}{2021}\right|\ge0;....;\left|\frac{x+2020}{2021}\right|\ge0\forall x\)
\(\Rightarrow\left|\frac{x+1}{2021}\right|+\left|\frac{x+2}{2021}\right|+...+\left|\frac{x+2020}{2021}\right|\ge0\forall x\)
\(\Rightarrow2021x\ge0\Rightarrow x\ge0\)
\(\Rightarrow\frac{x+1}{2021}+\frac{x+2}{2021}+...+\frac{x+2020}{2021}=2021x\)
\(\Rightarrow x+\frac{1}{2021}+x+\frac{2}{2021}+...+x+\frac{2020}{2021}=2021x\)
\(\Rightarrow2020x+\frac{1+2+...+2020}{2021}=2021x\)
\(\Rightarrow x=2020\)
I
5 tháng 1 2023
\(\dfrac{x+1}{2023}+\dfrac{x+2}{2022}=\dfrac{x+3}{2021}+\dfrac{x+4}{2020}\\ \Leftrightarrow\dfrac{x+1}{2023}+1+\dfrac{x+2}{2022}+1=\dfrac{x+3}{2021}+1+\dfrac{x+4}{2020}+1\\ \Leftrightarrow\dfrac{x+1+2023}{2023}+\dfrac{x+2+2022}{2022}-\dfrac{x+3+2021}{2021}-\dfrac{x+4+2020}{2020}=0\\ \Leftrightarrow\left(x+2024\right)\times\left(\dfrac{1}{2023}+\dfrac{1}{2022}-\dfrac{1}{2021}-\dfrac{1}{2020}\right)=0\\ \Rightarrow x+2024=0:\left(\dfrac{1}{2023}+\dfrac{1}{2022}-\dfrac{1}{2021}-\dfrac{1}{2020}\right)\\ \Rightarrow x+2024=0\\ \Rightarrow x=-2024\)
LD
30 tháng 10 2021
Ta có:
\(\frac{xy}{x+y}=\frac{yz}{y+z}=\frac{zx}{z+x}\rightarrow\frac{x+y}{xy}=\frac{y+z}{yz}=\frac{z+x}{zx}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}=\frac{1}{y}+\frac{1}{z}=\frac{1}{z}+\frac{1}{x}\Rightarrow\frac{1}{x}=\frac{1}{y}=\frac{1}{z}\Rightarrow x=y=z\)
Thay tất cả giá trị x,y,z vào M ta được:
\(M=\frac{2020x^3+2020y^3+2020z^3}{x^3+y^3+z^3}+\frac{2021x^5+2021y^5}{x^5+y^5}\)
\(\Rightarrow M=\frac{2020\left(x^3+y^3+z^3\right)}{x^3+y^3+z^3}+\frac{2021\left(x^5+y^5\right)}{x^5+y^5}\)
\(\Rightarrow M=2020+2021=4041\)
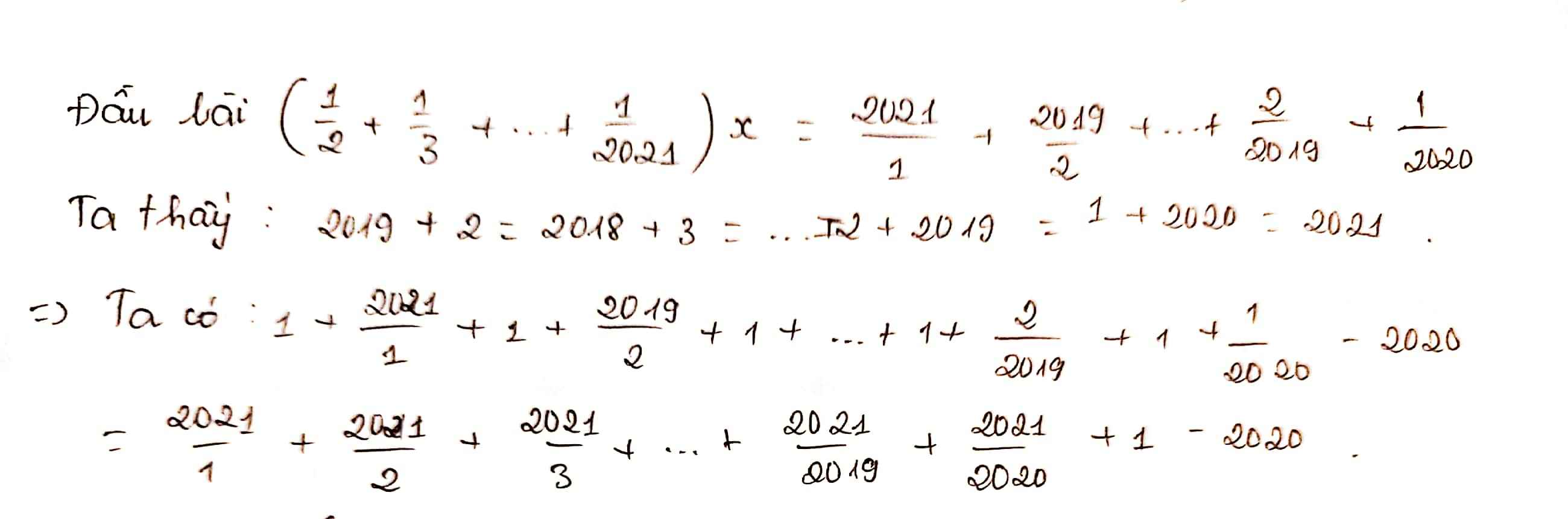
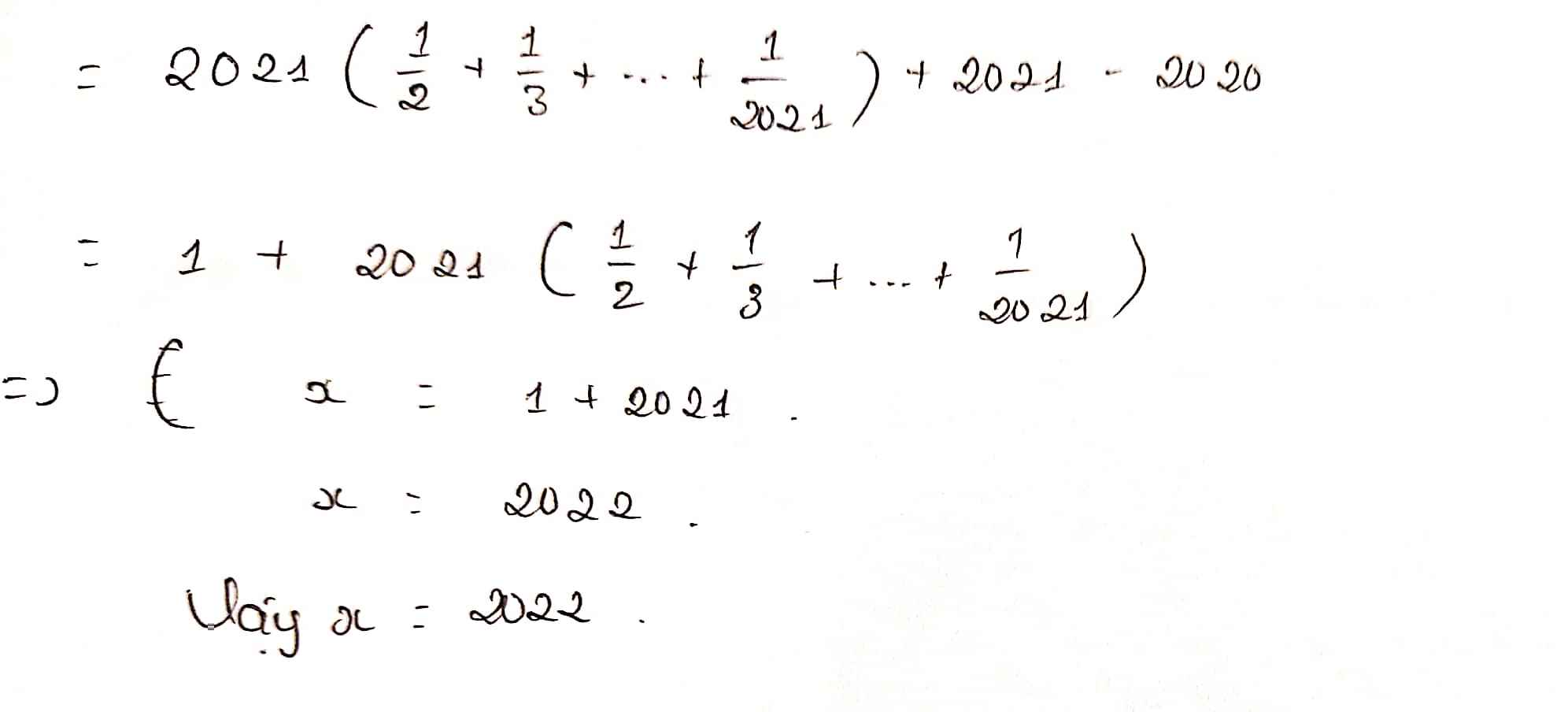
\(\dfrac{x+2}{2021}+\dfrac{x+3}{2020}=\dfrac{x+2021}{2}+\dfrac{x+2020}{3}\)
\(=>\dfrac{x+2}{2021}+1+\dfrac{x+3}{2020}+1=\dfrac{x+2021}{2}+1+\dfrac{x+2020}{3}+1\)
\(=>\dfrac{x+2+2021}{2021}+\dfrac{x+3+2020}{2020}=\dfrac{x+2021+2}{2}+\dfrac{x+2020+3}{3}\)
\(=>\dfrac{x+2023}{2021}+\dfrac{x+2023}{2020}-\dfrac{x+2023}{2}-\dfrac{x+2023}{3}=0\)
\(=>(x+2023)(\dfrac{1}{2021}+\dfrac{1}{2020}-\dfrac{1}{2}-\dfrac{1}{3})=0\)
Mà \(\dfrac{1}{2021}+\dfrac{1}{2020}-\dfrac{1}{2}-\dfrac{1}{3} \ne 0\)
\(=>x+2023=0\)
\(=>x=-2023\)
Thanks