Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ đường thẳng y = 2x -1 trên mặt phẳng tọa độ
Với x = 0 thì y = -1, ta được điểm A(0; -1) thuộc đồ thị hàm số y = 2x – 1
Với x = 1 thì y = 1, ta được điểm B(1; 1) thuộc đường thẳng y = 2x – 1
Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm A(0; -1) và điểm B(1; 1)
b) Vì đường thẳng y = ax + b \(\left( {a \ne 0} \right)\) song song với đường thẳng y = 2x -1 nên a = 2
Đường thẳng dã cho là: y = 2x + b
Vì đường thẳng y = 2x + b đi qua điểm M(1; 3) nên:
3 = 2.1 + b suy ra b = 1
Vậy đường thẳng cần tìm là; y = 2x + 1
* Vẽ đường thẳng y = 2x + 1
Với x = 0 thì y = 1, ta được điểm P(0, 1) thuộc đồ thị hàm số y = 2x + 1
Với x = 1 thì y = 1, ta được điểm Q(1; 3) thuộc đồ thị hàm số y = 2x + 1
Đồ thị hàm số y = 2x + 1 là đường thẳng đi qua hai điểm P(0; 1) và Q(1; 3)

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
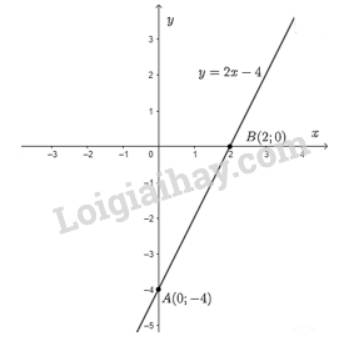
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

a: Thay x=1 và y=4 vào y=mx+1, ta được:
\(m\cdot1+1=4\)
=>m+1=4
=>m=3
b: Để hai đường thẳng này song song với nhau thì
\(\left\{{}\begin{matrix}m^2=m\\m\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m=0\\m\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\left(m-1\right)=0\\m\ne1\end{matrix}\right.\)
=>m=0

- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi chúng không có điểm chung.
- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi chúng có một điểm chung.
- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) trùng nhau khi chúng có vô số điểm chung.

a, Với \(m\ne2\)
d đi qua A(0;5) <=> \(m=5\)(tm)
b, (d1) : y = 2x + 3 nhé, mình đặt tên luôn ><
d // d1 <=> \(\hept{\begin{cases}m-2=2\\m\ne3\end{cases}}\Leftrightarrow\hept{\begin{cases}m=4\\m\ne3\end{cases}}\Leftrightarrow m=4\)

Đáp án đúng là C
Ta có: \(y = \dfrac{{ - x + 10}}{5} = \dfrac{{ - x}}{5} + \dfrac{{10}}{5} = \dfrac{{ - 1}}{5}x + 2\)
Vì hàm số \(y = \dfrac{{ - 1}}{5}x + 2\) có dạng \(y = ax + b\) nên đồ thị của hàm số là một đường thẳng với hệ số góc \(a = \dfrac{{ - 1}}{5}\).
Đồ thị hàm số cắt trục tung tại điểm \(A\left( {0;2} \right)\); Đồ thị hàm số cắt trục hoành tại điểm \(B\left( {10;0} \right)\).
Thay \(x = 200\) vào hàm số ta được: \(y = \dfrac{{ - 1}}{5}.200 + 2 = - 40 + 2 = - 38 \ne 50\). Do đó điểm \(\left( {200;50} \right)\)không thuộc đồ thị hàm số.
Vậy đáp án đúng là đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 10.

Đáp án đúng là C
Gọi đường thẳng cần tìm là \(d:y = ax + b\).
Vì đường thẳng \(d\) song song với đường thẳng \(y = 2x\) nên \(\left\{ \begin{array}{l}a = 2\\b \ne 0\end{array} \right.\)
Lại có, đường thẳng \(d\) cắt trục tung tại điểm có tung độ bằng 1 nên đường thẳng \(d\) đi qua điểm \(A\left( {0;1} \right)\). Do đó, \(b = 1 \ne 0\) (thỏa mãn).
Vậy đường thẳng \(d\) cần tìm là \(y = 2x + 1\).
a) Với �=−1m=−1, hàm số trở thành �=−2�+1y=−2x+1.
Xét hàm số �=−2�+1y=−2x+1 :
Thay �=0x=0 thì �=1y=1.
Suy ra đồ thị hàm số �=−2�+1y=−2x+1 đi qua điểm có tọa độ (0;1)(0;1).
Thay �=1x=1 thì �=−1y=−1.
Vì đường thẳng (�):�=��+�(d):y=ax+b song song với đường thẳng (�′ ):�=−3�+9(d′ ):y=−3x+9 nên: �≠−3;�≠9a=−3;b=9.
Khi đó ta có: (�):�=−3�+�(d):y=−3x+b và �≠9b
khác 9.
Vì đường thẳng (�):�=��+�(d):y=ax+b đi qua �(1;−8)A(1;−8) nên: −8=−3.1+�−8=−3.1+b
Suy ra �=−5b=−5 (thoả mãn)
Vậy đường thẳng cần tìm là (�):�=−3�−5(d):y=−3x−5.
Suy ra đồ thị hàm số �=−2�+1y=−2x+1 đi qua điểm có tọa độ (1;−1)(1;−1).
Vẽ đồ thị:
Vì đường thẳng (�):�=��+�(d):y=ax+b song song với đường thẳng (�′ ):�=−3�+9(d′ ):y=−3x+9 nên: �≠−3;�≠9a
khác−3;b
khác 9.
Khi đó ta có: (�):�=−3�+�(d):y=−3x+b và �≠9b
khác 9.
Vì đường thẳng (�):�=��+�(d):y=ax+b đi qua �(1;−8)A(1;−8) nên: −8=−3.1+�−8=−3.1+b
Suy ra �=−5b=−5 (thoả mãn)
Vậy đường thẳng cần tìm là (�):�=−3�−5(d):y=−3x−5.