K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
LQ
Lê Quốc Phú
3 tháng 4 2022

Bài toán về bất đẳng thưc lớp 8

a,Cho biết a<b. Hãy so sánh 2a-1 và 2b-1

b,Cho biết m>n. Hãy so sánh 7-3m và 7-3n
#Toán lớp 8
1
*•.¸♡ 𝓐𝓷𝓱𝓱 𝓣𝓱𝓾̛𝓾̛ ♡¸.•*
3 tháng 4 2022

a/ ta có : a<b

=> 2a<2b

=>2a-1<2b-1

 

Đúng(0)
BP
Boi Pin
19 tháng 3 2018 - olm

1. cho pt : 4x^2 -25 +x +4kx=0

a, giải pt với k= 0

b,tính x để x=-2 là ngiệm của pt

2.a, cho a.>2b+3

c/m 4a-5>8b+7

b, với a,b,c bất kì, c/m a^2 +b^2 +c^2 lớn hơn hoạc bằng ab+ac+bc

bài test của mình ^ ^, m n làm cho mình dò kết quả a

 

 
#Toán lớp 8
2
KT
Không Tên
19 tháng 3 2018

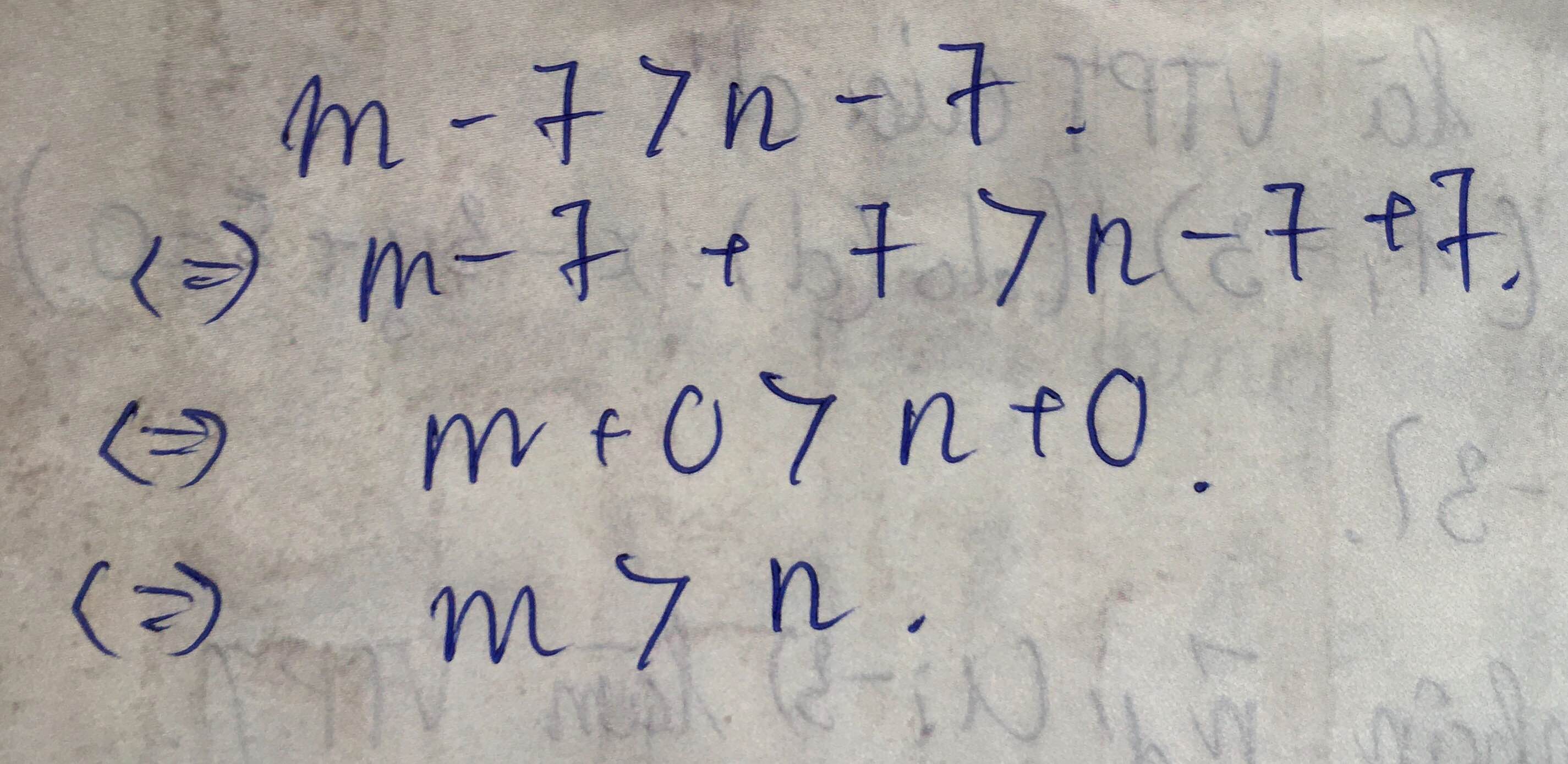
         \(a>2b+3\)

\(\Leftrightarrow\)\(4a>8b+12\)

\(\Leftrightarrow\)\(4a-5>8b+12-5\)

\(\Leftrightarrow\)\(4a-5>8b+7\) (đpcm)

Đúng(0)
KT
Không Tên
19 tháng 3 2018

        \(a^2+b^2+c^2\ge ab+bc+ca\)

 \(\Leftrightarrow\)\(a^2+b^2+c^2-ab-bc-ca\ge0\)

\(\Leftrightarrow\)\(2a^2+2b^2+2c^2-2ab-2bc-2ca\ge0\)

\(\Leftrightarrow\)\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)   (luôn đúng)

Dấu   "="  xảy ra  <=>  a = b = c

Đúng(0)
PC
Pi Chan
13 tháng 3 2017

Câu hỏi : Số b là số âm, số 0 , hay số dương nếu :

a) 5b > 3b

b ) -12b > 8b

c) -6b >= 9b

d) 3b =< 15b

. Giúp tớ nhie ;;-;;
#Toán lớp 8
1
TT
Trần Thị Ngọc Trâm
13 tháng 3 2017

a)ta có 5>3. để có bất đẳng thức cùng chiều 5b>3b ta phải nhân hai vế của bất phương trình 5>3 cho số dương. Vậy b là số dương

b)ta có -12<8 để có bất đẳng thức ngược chiều -12b>8b ta phải nhân hai vế của bất phương trình -12<8 cho số âm. vậy b âm

c)ta có -6=< 9 nên để có bất đẳng thức ngược chiều -6b>=9b ta phải nhân hai vế của bất phương trình -6=<9 cho số âm. vậy b âm

d) ta có 3=<15 để có bất đẳng thức cùng chiều 3b=<15b ta phải nhân hai vế của bất phương trình 3=<15 cho số dương. Vậy b là số dương

mình chưa học bài này nên cách giải không biết có đúng không nhưng kết quả chắc đúngok

Đúng(0)
3T
30.Nɠυұễɳ Tɦàɲɦ Pɦúƈ ヅ
24 tháng 4 2023
                                      Đề ôn tập HK 2 - Đề 8 Bài 1:a) Biết -3a - 1 > -3b - 1. So sánh a và b?b) Biết 4a + 3 < 4b + 3. So sánh a và b?Bài 2: Biết a < b, hãy so sánh:a) 3a - 7 và 3b - 7.                                b) 5 - 2a và 3 - 2bc) 2a + 3 và 2b + 3.                              d) 3a - 4 và 3b - 3Bài 3: a) Chứng minh pt: x² + 6x + 11 = 0 vô nghiệm          b) Chứng minh bất pt: 5x² + 16 ≥ 0 có vô số...
Đọc tiếp

                                      Đề ôn tập HK 2 - Đề 8

 

Bài 1:

a) Biết -3a - 1 > -3b - 1. So sánh a và b?

b) Biết 4a + 3 < 4b + 3. So sánh a và b?

Bài 2: Biết a < b, hãy so sánh:

a) 3a - 7 và 3b - 7.                                b) 5 - 2a và 3 - 2b

c) 2a + 3 và 2b + 3.                              d) 3a - 4 và 3b - 3

Bài 3: a) Chứng minh pt: x² + 6x + 11 = 0 vô nghiệm

          b) Chứng minh bất pt: 5x² + 16 ≥ 0 có vô số nghiệm.
#Toán lớp 8
1
MP
Minh Phương
24 tháng 4 2023

1.

a. -3a - 1 + 1 > -3b - 1 + 1 (cộng cả 2 vế cho 1)

  -3a . \(\left(\dfrac{-1}{3}\right)\) <  -3b . \(\left(\dfrac{-1}{3}\right)\) (nhân cả vế cho \(\dfrac{-1}{3}\) )

         a < b

b. 4a + 3 + (- 3) < 4b + 3 +(- 3) (cộng cả 2 vế cho -3)

   4a . \(\dfrac{1}{4}\) < 4b . \(\dfrac{1}{4}\) (nhân cả 2 vế cho \(\dfrac{1}{4}\) )

        a < b

2. 

a. Ta có: a < b 

3a < 3b ( nhân cả 2 vế cho 3)

3a - 7 < 3b - 7 (cộng cả 2 vế cho - 7 )

b. Ta có: a < b

-2a > -2b (nhân cả 2 vế cho -2)

5 - 2a > 5 - 2b ( cộng cẩ 2 vế cho 5)

c. Ta có: a < b 

2a < 2b (nhân cả vế cho 2)

2a + 3 < 2b + 3 (cộng cả 2 vế cho 3)

d. Ta có: a < b

3a < 3b (nhân cả 2 vế cho 3)

3a - 4 < 3b - 4 (cộng cả 2 vế cho -4)

Ta có: 3 < 4

đến đây ko bắt cầu qua đc chắc đề bài sai

 

 

 

Đúng(1)
VN
vi nguyễn
28 tháng 4 2019 - olm

1) / x-3/=9-2x

2) biết a -3 lớn hơn hoặc bằng b-3 so sánh a và b 

3) cho -3a  > - 3b so sánh a và b 
#Toán lớp 8
3
O
olm
28 tháng 4 2019

1)/x-3/=9-2x

/x-3/=\(\hept{\begin{cases}x-3khix>3\\3-xkhix< 3\end{cases}}\)

TH1:x>3 phương trình là 

           x-3=9-2x

<=>   x+2x=9+3

<=>   3x    =12

<=>     x    =4 (thỏa mãn)

TH2:x<3 phương trình là

       3-x=9-2x

<=>-x+2x=9-3

<=>x       =6(không thỏa mãn-loại)

Vậy tập nghiệm của phương trình là S={4}

Đúng(0)
O
olm
28 tháng 4 2019

2)từ a-3>=b-3

Cộng cả hai vế bất đẳng thức trên với 3 ta có

 a-3+3>=b-3+3

a>=b

Vậy a lớn hơn hoặc bằng b

Đúng(0)
M
Mimi
1 tháng 4 2018

Có bạn nào biết làm bài này ko ạ. Nếu biết thì giúp mình nhanh nhanh nhé, mình cảm ơn nhiều lắm

Bài 1: Áp dụng bất đẳng thức Cô Si chứng minh :

a) x/y + y/x lớn hơn hoặc bằng 2, với x, y>0

b) Cho a,b, c >0 ; a+b+c=1

Chứng minh 1/a + 1/b + 1/c lớn hơn hoặc bằng 9
#Toán lớp 8
1
KK
kuroba kaito
1 tháng 4 2018

a) áp dụng bđt cô si cho 2 số ta có

\(\dfrac{x}{y}+\dfrac{y}{x}\ge2\sqrt{\dfrac{x}{y}.\dfrac{y}{x}}\)

⇔ \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\) (đpcm )

b) áp dụng bđt cô si dạng phân số ta có

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{a+b+c}\)

⇔ \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge9\) (đpcm)

Đúng(0)
TT
Trương Thị Mỹ Trinh
15 tháng 5 2016 - olm

 

AI GIÚP MÌNH VỚI. MÌNH ĐANG GẤP LẮM.

a) Cho a > b. So sánh -3a và -3b

b) So sánh m-5 và m-7

c) Mẫu của một phân số lớn hơn tử số của nó là 3 đơn vị. Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới bằng 1/2. Tìm phân số ban đầu.
#Toán lớp 8
1
NM
NHỮNG MẢNH GHÉP CẢM XÚC
16 tháng 5 2016

a)   \(a>b\Rightarrow3a>3b\Rightarrow-3a<-3b\)

b) \(m-5>m-7\)

c)  Gọi phân số cần tìm là  \(\frac{a}{a+3}\)

Ta có     \(\frac{a+2}{a+5}=\frac{1}{2}\Rightarrow2a+4=a+5\Rightarrow2a-a=5-4\Rightarrow a=1\)

Vậy phân số cần tìm là   \(\frac{1}{4}\)

Đúng(0)
NM
Nguyen Manh Duc
4 tháng 7 2017 - olm

Cho tam giác ABC có a lớn hơn hoặc bằng b lớn hơn hoặc bằng c . So sánh a+ha ; b+hn ; c+hc
#Toán lớp 8
0
NT
nguyễn thị mai hương
11 tháng 11 2018 - olm
1 , xác định bài toán và viết giải thuật toán cho bài toán sau : tính diện tích hình A ( biết hình A được ghép từ một hình chữ nhật có chiều roongh : 20 , chiều dài : b , và một hình bán nguyệt có bán kính là a ) 2, cho 2 số thực a và b . cho biết kết quả so sánh hai số đó dưới dạng a lớn hơn b hoặc a nhỏ hơn b , hoặc a= b xác định bài toán và viết thuật toán cho bài toán trên đây là tin hok...
Đọc tiếp

1 , xác định bài toán và viết giải thuật toán cho bài toán sau : 

tính diện tích hình A ( biết hình A được ghép từ một hình chữ nhật có chiều roongh : 20 , chiều dài : b , và một hình bán nguyệt có bán kính là a ) 

2, cho 2 số thực a và b . cho biết kết quả so sánh hai số đó dưới dạng a lớn hơn b hoặc a nhỏ hơn b , hoặc a= b 

xác định bài toán và viết thuật toán cho bài toán trên 

đây là tin hok lớp 8 , giúp nhé , mai hok rùi , cần gấp lắm !!!!! 
#Toán lớp 8
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP