Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì N là trung điểm BD và AC nên ABCD là hbh
Vì M là trung điểm CE và AB nên AEBC là hbh
b, Vì ABCD và AEBC là hbh nên \(\left\{{}\begin{matrix}AE//BC;AE=BC\\AD//BC;AD=BC\end{matrix}\right.\Rightarrow AE\equiv AD;AE=AD\)
Vậy E đx D qua A

a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
b: Xét tứ giác AEBC có
N là trung điểm chung của AB và EC
nên AEBC là hình bình hành
=>AE//BC và AE=BC
=>AD//AE và AD=AE
=>A là trung điểm của DE

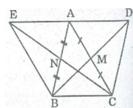
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
xét tam giác ADE có:
AB=DB( gt)
AC=EC (gt)
=> BC//DE ( t/c đường trung bình)
ta có: BC//DE (CMT)
AM vuông góc với BC
AM=IM
=> góc AID= góc AIE
Xét tam giác AEI và tam giác ADIcó:
góc DAI= góc EAI
AI chung
góc AID= góc AIE (CMT)
=> tam giác AEI = tam giác ADI (g.c.g)
=> DI=EI(2 cạnh tương ứng)

a. tam giác ABC có AM=MC và BN=NC => MN là đg TB của ABC => MN//AB => AMNB là hình thang ( k thể là Hình bình hành được )
b. D là điểm đối xứng với B qua M =>BM=MD
Tứ giác ABCD có AM=MC và BM=MD => 2 đg chéo cắt nhau tại trung điểm của mỗi đường
=> ABCD là HBH
c. E đối xứng với A qua N => AN=NE
ABEC có BN=NC và AN=NE => ABEC là HBH ( CMTT như câu b )

a: Xét tứ giác AEBM có
D là trung điểm của AB
D là trung điểm của EM
Do đó: AEBM là hình bình hành

a, Vì M là trung điểm AC và BE nên ABCE là hbh
b, Vì ABCE là hbh nên AE//BC;AE=BC(1)
Vì N là trung điểm AB và CF nên ACBF là hbh
Do đó AF//BC;AF=BC(2)
Từ (1)(2) ta được AE trùng AF và AE=AF
Vậy E đx F qua A

a: Xét tứ giác ABCE có
M là trung điểm của AC
M là trung điểm của BE
Do đó: ABCE là hình bình hành

Xét tứ giác ABCD có
AM=CM; BM=DM => ABCD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AD//=BC
Xét ứ giác ACBE có
AN=BN; CN=EN => ACBE là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AE//=BC
=> AD=AE =BC
=> AE trùng AD hay A; D; E thẳng hàng (Qua 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
=> D đối xứng với E qua A
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
a. Vì tam giác ABC có trung tuyến BM (gt)
-> M là trung điểm AC
Vì D đối xứng với B qua M (gt)
-> M là trung điểm BD
xét tứ giác ABCD có : - M là trung điểm AC (cmt)
- M là trung điểm BD (cmt)
=> tứ giác ABCD là hình bình hành
b) Vì tam giác ABC có trung tuyến CN(gt)
-> N là trung điểm AB
Vì E đối xứng với C qua N (gt)
-> N là trung điểm EC
xét tứ giác AEBC có : - N là trung điểm AB (cmt)
- N là trung điểm EC (cmt)
-> tứ giác AEBC là hình bình hành
=> AE // BC ( tính chất )
c)Vì tứ giác ABCD là hình bình hành ( cmt )
-> AD = BC (tính chất) (1)
Vì tứ giác AEBC là hình bình hành ( cmt )
-> AE = BC (2)
từ (1) và (2) => AE = AD
=> A là trung điểm ED
=> E đối xứng vói D qua A