Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 4 số cần tìm lần lượt là \(a,b,c,d\) Theo bài ra ta có :\(\begin{cases}a=3c\\b=2c\\d=b+7\\a+b+c+d=143\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a-3c=0\\b-2c=0\\b-d=-7\\a+b+c+d=143\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a=51\\b=34\\c=17\\d=41\end{cases}\) (bấm máy hpt 4 ẩn)
Vậy 4 số cần tìm lần lượt là \(51;34;17;41\)

ta có a/b=3/5 nên a=3/5b
ta có a+15/b=9/10 suy ra (a+15)*10=9b
10a+150=9b
10*(3/5b)+150=9b
30b/5+150=9b
6b+150=9b
150=9b-6b
150=3b
b=50
a=3/5*50=30

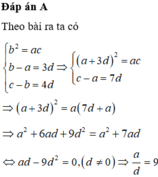




a/5 =b/9
a/10 =c/7
=> a/10 = b/18 =c/7 = k
=> a= 10k; b=18k; c=7k
=> BSCNN (a,b,c) = BSCNN (10k, 18k, 7k) = 630k [BSC của 10, 18, 7 là 630]
=> k=10
=> a=100; b =180, c=70