Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) đK: \(x\ne0;2\)
B = \(\dfrac{3x-4}{x\left(x-2\right)}.\dfrac{x\left(x-2\right)}{x^2-4-x^2}=\dfrac{3x-4}{-4}=\dfrac{4-3x}{4}\) \(\dfrac{x-4+2x}{x\left(x-2\right)}:\dfrac{\left(x-2\right)\left(x+2\right)-x^2}{x\left(x-2\right)}\)
= \(\dfrac{3x-4}{x\left(x-2\right)}.\dfrac{x\left(x-2\right)}{x^2-4-x^2}=\dfrac{4-3x}{4}\)
b) Thay x = -2 (TMDK) vào B, ta có:
\(B=\dfrac{4-3.\left(-2\right)}{4}=\dfrac{4+6}{4}=\dfrac{5}{2}\)
c) Để \(\left|B\right|-2x=5\)
<=> \(\left|\dfrac{4-3x}{4}\right|-2x=5\)
TH1: \(x\le\dfrac{4}{3}\)
<=> \(\left|\dfrac{4-3x}{4}\right|=\dfrac{4-3x}{4}\)
PT <=> \(\dfrac{4-3x}{4}-2x=5\)
<=> \(\dfrac{4-3x-8x}{4}=5\)
<=> \(4-11x=20\)
<=> x = \(\dfrac{-16}{11}\) (Tm)
TH2: \(x>\dfrac{4}{3}\)
<=> \(\left|\dfrac{4-3x}{4}\right|=\dfrac{3x-4}{4}\)
PT <=> \(\dfrac{3x-4}{4}-2x=5\)
<=> \(\dfrac{3x-4-8x}{4}=5\)
<=> \(-5x-4=20\)
<=> \(x=\dfrac{-24}{5}\left(l\right)\)
d) Xét (2-x)B = \(\dfrac{\left(2-x\right)\left(4-3x\right)}{4}\) = \(\dfrac{3x^2-10x+8}{4}\)
= \(\dfrac{3\left(x-\dfrac{5}{3}\right)^2-\dfrac{1}{3}}{4}\)
Mà \(3\left(x-\dfrac{5}{3}\right)^2\ge\) 0
=> (2-x)B \(\ge\dfrac{\dfrac{-1}{3}}{4}=\dfrac{-1}{12}\)
Dấu "=" <=> x = \(\dfrac{5}{3}\left(tm\right)\)
e) Số nguyên âm lớn nhất là -1
Để B = -1
<=> \(\dfrac{4-3x}{4}=-1\)
<=> 4 - 3x = -4
<=> \(x=\dfrac{8}{3}\left(tm\right)\)
g)
TH1: \(x\le\dfrac{4}{3}\)
<=> \(\left|\dfrac{4-3x}{4}\right|=\dfrac{4-3x}{4}\)
BDT <=> \(\dfrac{4-3x}{4}< 2x-4\)
<=> \(4-3x< 8x-16\)
<=> \(x>\dfrac{20}{11}\left(l\right)\)
TH2: \(x>\dfrac{4}{3}\)
<=> \(\left|\dfrac{4-3x}{4}\right|=\dfrac{3x-4}{4}\)
BDT <=> \(\dfrac{3x-4}{4}< 2x-4\)
<=> \(3x-4< 8x-16\)
<=> x > \(\dfrac{12}{5}\)
KHDK: \(x>\dfrac{12}{5}\)

a,ĐK: \(\hept{\begin{cases}x\ne0\\x\ne\pm3\end{cases}}\)
b, \(A=\left(\frac{9}{x\left(x-3\right)\left(x+3\right)}+\frac{1}{x+3}\right):\left(\frac{x-3}{x\left(x+3\right)}-\frac{x}{3\left(x+3\right)}\right)\)
\(=\frac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\frac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)
\(=\frac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}.\frac{3x\left(x+3\right)}{-x^2+3x-9}=\frac{-3}{x-3}\)
c, Với x = 4 thỏa mãn ĐKXĐ thì
\(A=\frac{-3}{4-3}=-3\)
d, \(A\in Z\Rightarrow-3⋮\left(x-3\right)\)
\(\Rightarrow x-3\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\Rightarrow x\in\left\{0;2;4;6\right\}\)
Mà \(x\ne0\Rightarrow x\in\left\{2;4;6\right\}\)

\(B=\dfrac{3\left(x+1\right)}{x^3+x^2+x+1}=\dfrac{3\left(x+1\right)}{x^2\left(x+1\right)+\left(x+1\right)}=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x^2+1\right)}=\dfrac{3}{x^2+1}\)
Do \(x^2\ge0\forall x\Rightarrow x^2+1\ge1\forall x\)
\(\Rightarrow B=\dfrac{3}{x^2+1}\le\dfrac{3}{1}=3\)
\(maxB=3\Leftrightarrow x^2=0\Leftrightarrow x=0\)

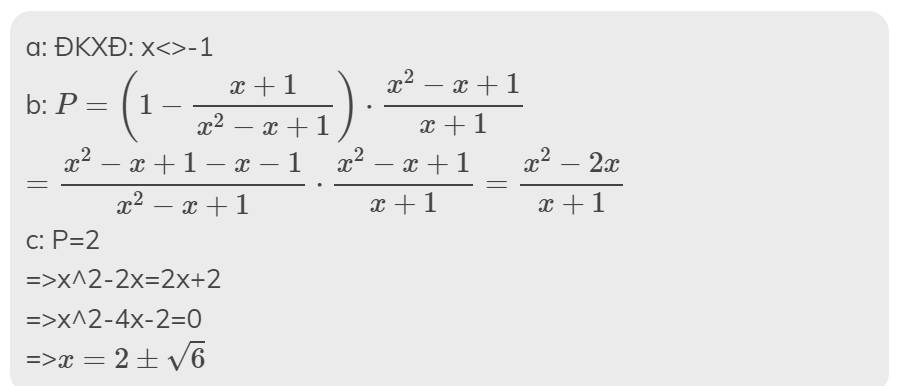
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)

Biểu thức không có max. Bạn coi lại đề.
Dạ vâng