Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để \(A = B\)
\(\begin{array}{l} \Leftrightarrow \left\{ {5;x} \right\} = \left\{ {2;5} \right\}\\ \Leftrightarrow x = 2\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}A = C \\\Leftrightarrow \left\{ {2;y} \right\} = \left\{ {2;5} \right\} \\ \Leftrightarrow y = 5\end{array}\)
Vậy \(x = 2;y = 5\) thì \(A = B = C\).

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)

\(a,\)\(A=\left\{x\in R|x< 3\right\}\Rightarrow A=\left(\text{ -∞;3}\right)\)
\(B=\left\{-1;0;1;2;3;4;5\right\}\)
\(\Rightarrow A\cap B=\left\{-1;0;1;2\right\}\)
\(b,x=-1\Rightarrow y=1-2\left(-1\right)+m=m+3\)
\(x=1\Rightarrow y=1-2+m=m-1\)
\(\Rightarrow C=(m-1;m+3]\subset A\)
\(\Rightarrow C\subset A\Leftrightarrow m+3< 3\Leftrightarrow m< 0\)

a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:

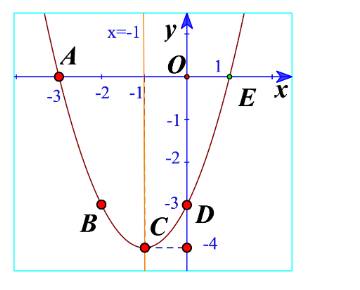
b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.