
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1.
$A=2+2^2+2^3+2^4+...+2^{10}$
$=(2+2^2+2^3+2^4)+(2^5+2^6+2^7+2^8)+2^9+2^{10}$
$=2(1+2+2^2+2^3)+2^5(1+2+2^2+2^3)+2^9(1+2)$
$=15(2+2^5)+3.2^9$
Ta thấy $15(2+2^5)\vdots 5$ còn $3.2^9\not\vdots 5$
$\Rightarrow A\not\vdots 5$
Bài 2:
$B=2+2^2+2^3+2^4+...+2^{99}+2^{100}$
$=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+...+2^{99}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{99})$
$=3(2+2^3+2^5+...+2^{99})\vdots 3$

Không nên đăng những thứ này nhưng chúng ta có thể nói chuyện với nhau mà

3.
\(C=5+5^2+...+5^6\\ C=5\left(1+5\right)+5^3\left(1+5\right)+5^5\left(1+5\right)\\ C=5\cdot6+5^3\cdot6+5^5\cdot6\\ C=6\left(5+5^3+5^5\right)\\ =>C⋮6\)
\(4.D=3+3^2+...+3^6\\D=3\left(1+3\right)+3^3\left(1+3\right)+3^5\left(1+3\right)\\ D=3\cdot4+3^3\cdot4+3^5\cdot5\\ C=4\left(3+3^3+3^5\right)\\ =>D⋮4\\ 5.E=4+4^2+...+4^6\\ E=4\left(1+4\right)+4^3\left(1+4\right)+4^5\left(1+4\right)\\ E=4\cdot5+4^3\cdot5+4^5\cdot5\\ E=5\left(4+4^3+4^5\right)=>E⋮5 \)


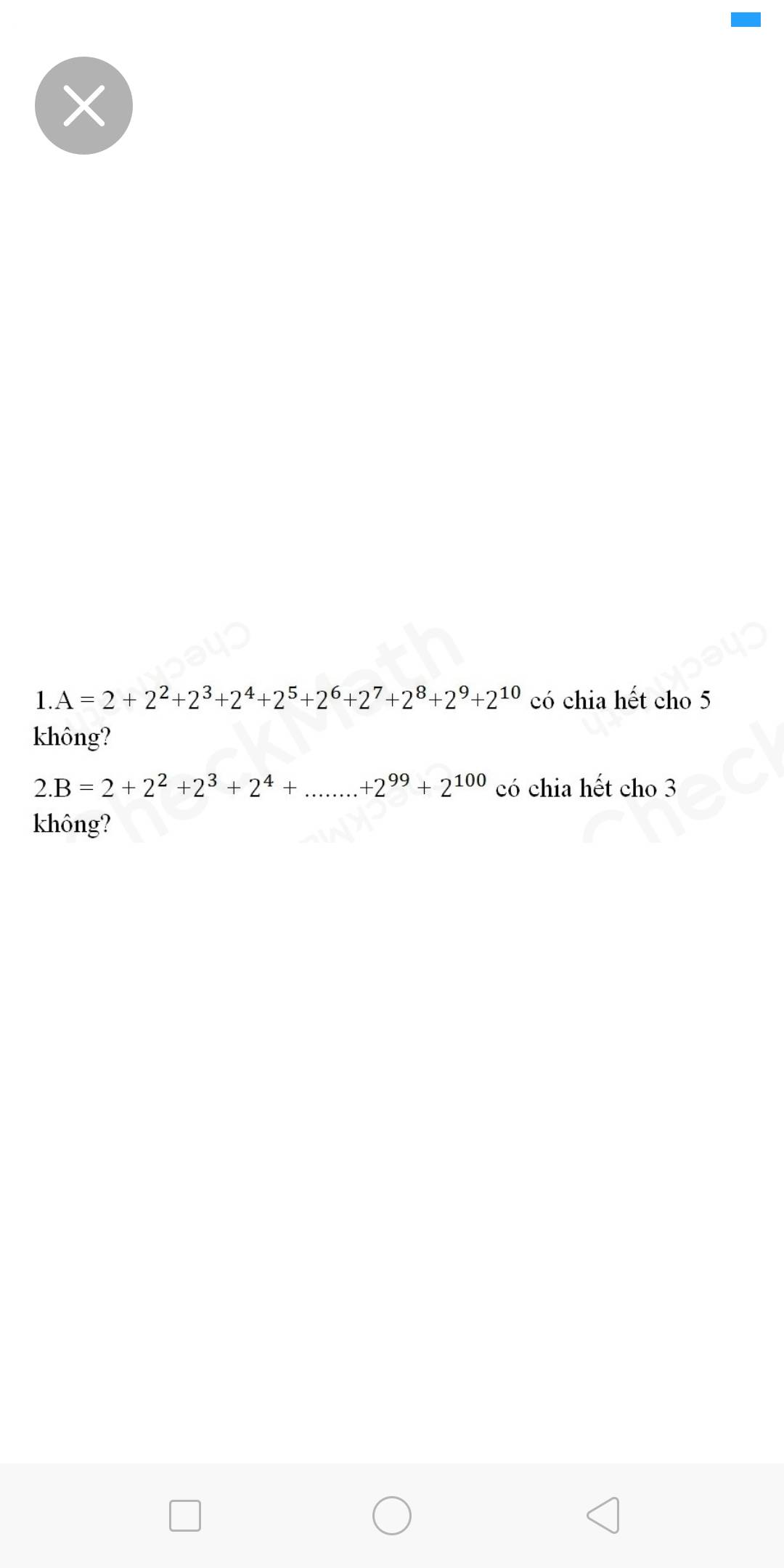





mk đk hơm