K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
20 tháng 2 2022
Lời giải:
$\Delta'=(m-1)^2-(m+1)=m^2-3m=m(m-3)$
Áp dụng định lý Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=2(m-1)$
$x_1x_2=m+1$
a. Để pt có 2 nghiệm trái dấu thì \(\left\{\begin{matrix} \Delta '>0\\ x_1x_2<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-3)>0\\ m+1<0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m>3 \text{or} m< 0\\ m< -1\end{matrix}\right.\Leftrightarrow m< -1\)
b. Có 2 nghiệm pb khi mà $\Delta'=m(m-3)>0$
$\Leftrightarrow m>3$ hoặc $m< 0$
c.
Có 2 nghiệm dương pb khi mà \(\left\{\begin{matrix} \Delta'>0\\ x_1+x_2>0\\ x_1x_2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-3)>0\\ 2(m-1)>0\\ m+1>0\end{matrix}\right.\Leftrightarrow m>3\)
d.
PT có 1 nghiệm dương khi mà:
TH1: Nó có 2 nghiệm trái dấu (kết quả giống phần a)
TH2: Nó có 1 nghiệm kép dương. Có nghiệm kép khi mà $\Delta'=0\Leftrightarrow m=0$ hoặc $m=3$
Thay lần lượt 2 giá trị này vô pt ban đầu suy ra $m=3$
TH3: Nó có 1 nghiệm dương 1 nghiệm =0
PT có nghiệm $=0\Leftrightarrow 0^2-2(m-1).0+m+1=0$
$\Leftrightarrow m=-1$
Thay trở lại pt ban đầu thì nghiệm còn lại $=-4<0$ (loại)
Vậy...........
21 tháng 2 2022
Khổ thơ thứ 2 ,3đã diễn tả những cảm nhân tinh tế của nhà thơ về những biến chuyển của đất trời trong khoảnh khắc giao mùa. Đến đây, nhà thơ không còn những mơ hồ, hoài nghi về khí thu se lạnh đã chạm ngõ. Thiên nhiên sang thu đã được cụ thể bằng những hình ảnh: “sông dềnh dàng”, “chim vội vã”, “đám mây vắt nửa mình”. Bằng phép nhân hóa đặc sắc, nhà thơ đã rất tài hoa ghi lại linh hồn của cảnh vật, của dòng sông quê hương nơi vùng đồng bằng Bắc Bộ ăm ắp nước phù sa. Cái dềnh dàng của sông là sau lúc vượt thác leo ghềnh nhọc nhằn , đã đến lúc được nghỉ ngơi sau bao mùa mưa lũ. Còn bầy chim, khi mùa thu chợt đến, nó phải gấp gáp để làm tôt tha mồi. Câu thơ cho thấy 2 tốc độ trái chiều giữa dòng sông và cánh chim, cũng là quy luật không đồng đều ở vào thời điểm giao thoa của muôn vật muôn loài. Sự chuyển mình sang thu không chỉ được biểu hiện qua sự đối lập trong hoạt động của con sông, cánh chim mà cón thể hiện rõ nét hơn cả quan hình ành "Cóđám mây mùa hạ/Vắt nửa mình sang thu". Hữu Thỉnh dùng động từ “vắt” để gợi ra trong thời điểmgiao mùa, đám mây như kéo dài ra, nhẹ trôi như tấm lụa mềm treo lơ lửng giữabầu trời trong xanh, cao rộng. Mùa ha, mùa thu là 2 đầu bến và đám mây là nhịp cầu vắt qua. Cái tài của Hữu Thỉnh là dùng không gian để miêu tả thời gian, làm hiện rõ ranh giới từ hạ snag thu vốn mong manh trở nên cụ thể, hữu hình. Đám mây là nhịp cầu duyên dáng nối 2 bờ thời gian bằng vẻ đpẹ mềm mại, trữ tình. Qua cách cảm nhận ấy, ta thấy Hữu Thỉnh có một hồn thơ nhạy cảm, yêu thiên nhiên tha thiết, một trí tưởng tượng bay bổng.
19 tháng 11 2023
ĐKXĐ: \(\left\{{}\begin{matrix}2x+5>=0\\4-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x>=-5\\2x< =4\end{matrix}\right.\Leftrightarrow-\dfrac{5}{2}< =x< =2\)
\(x^2+\sqrt{2x+5}+\sqrt{4-2x}=4x-1\)
=>\(x^2-4+\sqrt{2x+5}-3+\sqrt{4-2x}=4x-1-7\)
=>\(\left(x-2\right)\left(x+2\right)+\dfrac{2x+5-9}{\sqrt{2x+5}+3}+\sqrt{4-2x}=4x-8\)
=>\(\left(x-2\right)\left[\left(x+2\right)+\dfrac{2}{\sqrt{2x+5}+3}-4\right]+\sqrt{4-2x}=0\)
=>\(-\left(2-x\right)\left[\left(x-2\right)+\dfrac{2}{\sqrt{2x+5}+3}\right]+\sqrt{2\left(2-x\right)}=0\)
=>\(\sqrt{2-x}\left[-\sqrt{2-x}\left(x-2+\dfrac{2}{\sqrt{2x+5}+3}\right)+\sqrt{2}\right]=0\)
=>\(\sqrt{2-x}=0\)
=>x=2(nhận)
19 tháng 8 2021
Bài 2:
Áp dụng định lí Pytago vào ΔEFG vuông tại E, ta được:
\(FG^2=EF^2+EG^2\)
\(\Leftrightarrow FG^2=15^2+5^2=250\)
hay \(FG=5\sqrt{10}\left(cm\right)\)
F
26 tháng 5 2019
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
17 tháng 1 2023
góc ABE+góc A=90 độ
góc ACF+góc A=90 độ
=>góc ABE=góc ACF
7 tháng 6 2021
PT có 2 nghiệm phân biệt
`<=>(4m+3)^2-8(2m^2-1)>0`
`<=>16m^2+24m+9-16m^2+8>0`
`<=>24m+17>0`
`<=>24m> -17`
`<=>m>(-17)/24`
PT có 1 nghiệm =1 thì ta thay x=1 thì pt =
`=>2.1-(4m+3).1+2m^2-1=0`
`<=>2m^2-1-(4m+3)+2=0`
`<=>2m^2+1-4m-3=0`
`<=>2m^2-4m-2=0`
`<=>m^2-2m-1=0`
`a=1,b=-2,c=-1`
`Delta'=1+1=2`
`=>x_1=1+sqrt2(tm),1-sqrt2(tm)`
Vậy `m=1+-sqrt2` thì PT có 2 nghiệm phân biệt có 1 nghiệm = 1
TA
7 tháng 6 2021
PT có 1 nghiệm là `1 <=> 2-(4m+3)+2m^2-1=0`
`<=> 2m^2-4m-2=0`
`<=>m=1 \pm \sqrt2`.
29 tháng 8 2021
Bài 4:
a: ĐKXĐ: \(x\ge\dfrac{3}{2}\)
b: ĐKXĐ: x>1
c: ĐKXĐ: x<-2
d: ĐKXĐ: \(x>2\)
e: ĐKXĐ: \(x< \dfrac{5}{2}\)
f: ĐKXĐ: \(x\ge2\)
24 tháng 2 2021
2x2 - ( m + 4 )x + m = 0
Δ = b2 - 4ac = ( m + 4 )2 - 8m = m2 + 8m + 16 - 8m = m2 + 16
Vì m2 + 16 ≥ 16 > 0 ∀ m => Δ ≥ 16 > 0
Vậy phương trình luôn có nghiệm ( đpcm )
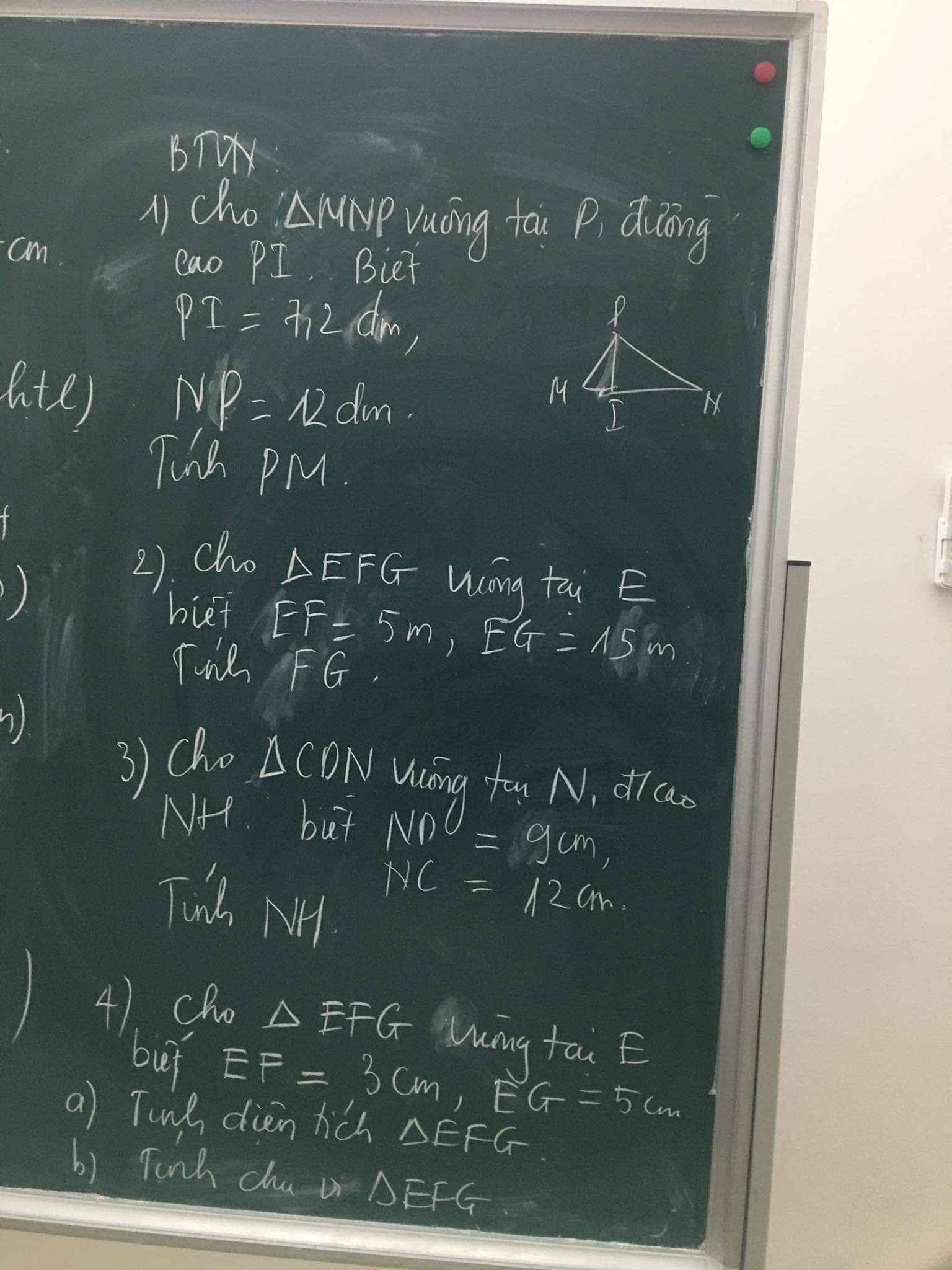
45) \(\sqrt{\left(3-\sqrt{5}\right)^2}=\left|3-\sqrt{5}\right|=3-\sqrt{5}\)
47) \(\sqrt{8+2\sqrt{15}}=\sqrt{3+2\sqrt{15}+5}=\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}=\sqrt{5}+\sqrt{3}\)
48) \(\sqrt{23+4\sqrt{15}}=\sqrt{3+4\sqrt{15}+20}=\sqrt{\left(\sqrt{3}+2\sqrt{5}\right)^2}=\sqrt{3}+2\sqrt{5}\)
49) \(\sqrt{11+4\sqrt{6}}=\sqrt{3+4\sqrt{6}+8}=\sqrt{\left(\sqrt{3}+2\sqrt{2}\right)^2}=\sqrt{3}+2\sqrt{2}\)
50) \(\sqrt{14-6\sqrt{5}}=\sqrt{9-6\sqrt{5}+5}=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
51) \(\sqrt{22-8\sqrt{6}}=\sqrt{16-8\sqrt{6}+6}=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
52) \(\sqrt{16-6\sqrt{7}}=\sqrt{9-6\sqrt{7}+7}=\sqrt{\left(3-\sqrt{7}\right)^2}=3-\sqrt{7}\)
53) \(\sqrt{9-4\sqrt{2}}=\sqrt{8-4\sqrt{2}+1}=\sqrt{\left(2\sqrt{2}-1\right)^2}=2\sqrt{2}-1\)
54) \(\sqrt{13-4\sqrt{3}}=\sqrt{12-4\sqrt{3}+1}=\sqrt{\left(2\sqrt{3}-1\right)^2}=2\sqrt{3}-1\)
55) \(\sqrt{7-4\sqrt{3}}=\sqrt{4-4\sqrt{3}+3}=\sqrt{\left(2-\sqrt{3}\right)^2}=2-\sqrt{3}\)
56) \(\sqrt{21-8\sqrt{5}}=\sqrt{16-8\sqrt{5}+5}=\sqrt{\left(4-\sqrt{5}\right)^2}=4-\sqrt{5}\)
57) \(\sqrt{\frac{9}{4}-\sqrt{2}}=\sqrt{\frac{1}{4}-\sqrt{2}+2}=\sqrt{\left(\frac{1}{2}-\sqrt{2}\right)^2}=\sqrt{2}-\frac{1}{2}\)
58) \(\sqrt{\frac{129}{16}+\sqrt{2}}=\sqrt{8+\sqrt{2}+\frac{1}{16}}=\sqrt{\left(2\sqrt{2}+\frac{1}{4}\right)^2}=2\sqrt{2}+\frac{1}{4}\)
59) \(\sqrt{3+\sqrt{8}}=\sqrt{2+2\sqrt{2}+1}=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
60) \(\sqrt{2}\sqrt{8+3\sqrt{7}}=\sqrt{16+6\sqrt{7}}=\sqrt{9+6\sqrt{7}+7}=\sqrt{\left(3+\sqrt{7}^2\right)}=3+\sqrt{7}\)