K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 1 2022
a, 4,78+x=5,6 <=> x=5,6-4,78 = 0,82
b, x-3,92=0,61 <=> x = 3,92 + 0,61 = 4,53
c, 7-x=4,52 <=> x = 7-4,52 = 2,48
23 tháng 1 2022
a: =>x=5,6-4,78=0,82
b: =>x=0,61+3,92=4,53
c: =>x=7-4,52=2,48
d: =>x=17,1:4,5=3,8
e: =>x=17,1x4,5=76,95
f: =>x=42,16:6,2=6,8
AT
28 tháng 5 2023
Thời gian đi từ A đến B với vận tốc 12 km/h là:
45 : 12 = 3,75 (giờ)
= 3 giờ 45 phút
Vậy người đó phải khởi hành lúc:
11 giờ 10 phút - 3 giờ 45 phút = 7 giờ 25 phút
Đ/s:...........
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 6 2023
2. So sánh: A = \(\dfrac{1}{41}\) + \(\dfrac{1}{42}\) + \(\dfrac{1}{43}\) + \(\dfrac{1}{44}\)+...+ \(\dfrac{1}{80}\) và B = \(\dfrac{7}{12}\)
\(\dfrac{1}{41}>\dfrac{1}{42}>\dfrac{1}{43}>...>\dfrac{1}{60}\)
Xét mẫu số các phân số trên lần lượt là các số thuộc dãy số sau:
41; 42; 43;...;60
Dãy số trên là dãy số cách đều với khoảng cách là: 42 - 41 =1
Số số hạng của dãy số trên là: (60 - 41):1 + 1 = 20
⇒ \(\dfrac{1}{41}\) + \(\dfrac{1}{42}\)+...+ \(\dfrac{1}{60}\) > \(\dfrac{1}{60}\) \(\times\) 20 = \(\dfrac{1}{3}\) (1)
Chứng minh tương tự ta cũng có:
\(\dfrac{1}{61}+\dfrac{1}{62}+...+\dfrac{1}{80}\) > \(\dfrac{1}{80}\) \(\times\) 20 = \(\dfrac{1}{4}\) (2)
Kết hợp(1) và (2) ta có:
A = \(\dfrac{1}{41}+\dfrac{1}{42}+\dfrac{1}{43}+\dfrac{1}{44}+...+\dfrac{1}{80}\) > \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\) = \(\dfrac{7}{12}\)
Vậy A > B
14 tháng 11 2021
118:
80,71. 658,53. 613,72. 754.58
119:
a)55,24
b)238,932
c)613,545
d)563,552
120:
a)28,16
b)87,71
c)27,9
d)599,1
Làm hết sạch các câu bạn gửi à bạn
AH
Akai Haruma
Giáo viên
4 tháng 3 2023
Lời giải:
Thể tích của bể:
$4\times 3\times 0,5=6$ (m3)
Đổi $6$ m3 = $6000$ lít.
Mỗi phút cả 2 vòi chảy được: $85+25=110$ (lít)
Nếu cả hai vòi cùng chảy thì sẽ đầy bể sau:
$6000:110=\frac{600}{11}$ (phút)
11 tháng 7 2016
20+3.x=110
3.x=110-20
3.x=90
x=90:3
x=30
LƯU Ý: DẤU "." LÀ DẤU NHÂN
11 tháng 7 2016
\(20+3\times x=110\)
\(3\times x=110-20=90\)
\(x=90:3=30\)
NT
3
5 tháng 5 2021
x x 8 + x x 2 = 34,8
x x ( 8 + 2) = 34,8
x x 10 = 34,8
x = 34,8 : 10
x = 3,48
5 tháng 5 2021
X x 8 + X x 2 = 34 x 8
X x ( 8 + 2 ) = 272
X x 10 = 272
X = 272 : 10
X = 27,2
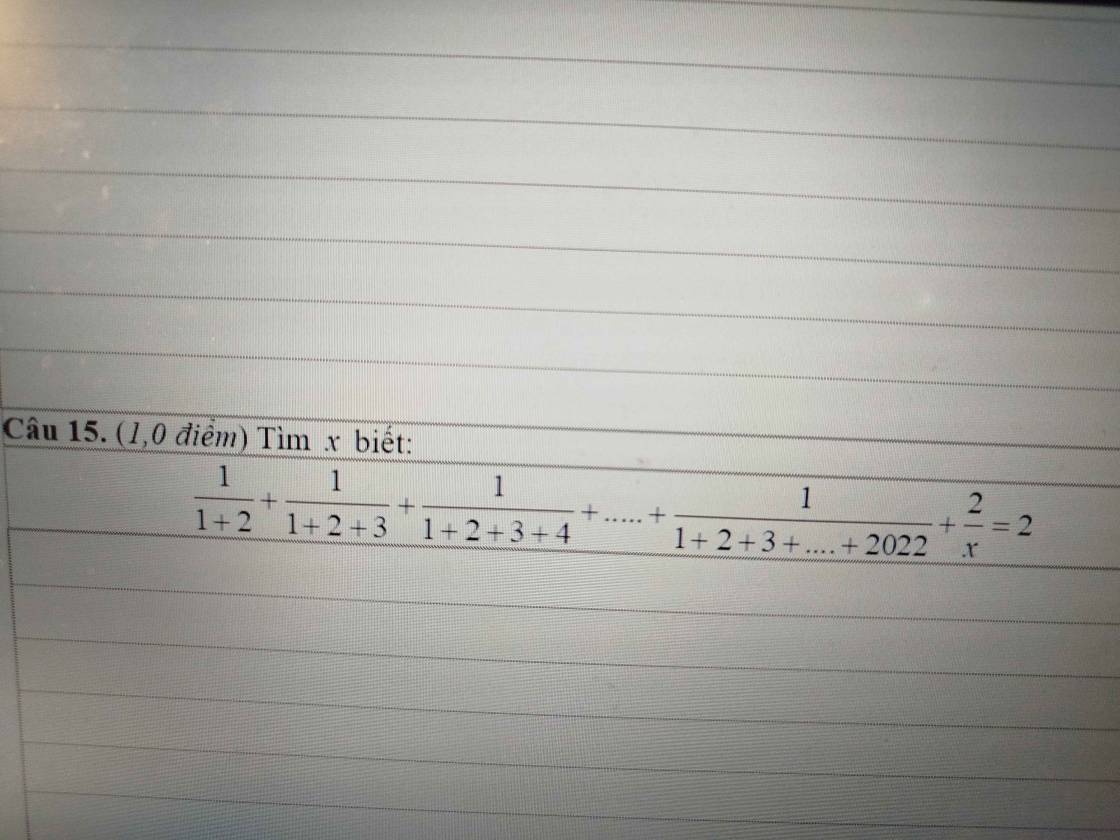
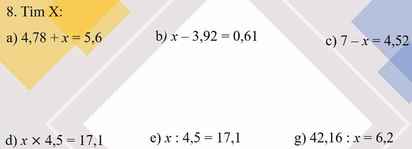
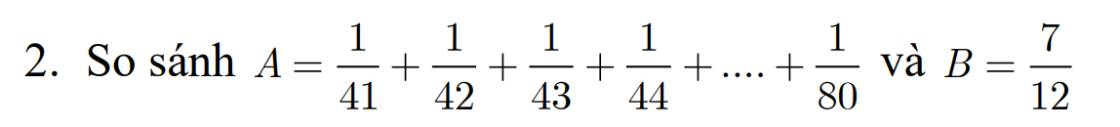
\(\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2022}+\dfrac{2}{x}=2\)
=>\(\dfrac{1}{2\text{x}\dfrac{3}{2}}+\dfrac{1}{3\text{x}\dfrac{4}{2}}+...+\dfrac{1}{2022\text{x}\dfrac{2023}{2}}+\dfrac{2}{x}=2\)
=>\(\dfrac{2}{2\text{x}3}+\dfrac{2}{3\text{x}4}+...+\dfrac{2}{2022\text{x}2023}+\dfrac{2}{x}=2\)
=>\(\dfrac{1}{2\text{x}3}+\dfrac{1}{3\text{x}4}+...+\dfrac{1}{2022\text{x}2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{2}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{x}+\dfrac{2021}{4046}=1\)
=>\(\dfrac{1}{x}=1-\dfrac{2021}{4046}=\dfrac{2025}{4046}\)
=>\(x=\dfrac{4046}{2025}\)