K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
2
Ai ai giúp với Ạ!
S
15 tháng 8 2021
a) ta có:tg AMB =TG AMC suy ra AB= AC suy ra tg ABC cân tại A
suy ra BM=MC suy ra AM là đưòng trung tuyến tg ABC
Mà tg ABC cân tại A suy ra AM là pg góc A( tính chất tg cân)
b) suy ra AM là đưòng cao tg ABC (tính chất tg cân)
suy ra AM vuông góc BC.
Đây nè bạn!!!!
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Bài 3:
Gọi $a,b,c$ là độ dài ba cạnh tam giác theo thứ tự tăng dần. Theo bài ra ta có:
$\frac{a}{3}=\frac{b}{5}=\frac{c}{7}$ và $c+a-b=20$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a-b+c}{3-5+7}=\frac{20}{5}=4$
$\Rightarrow a=3.4=12; b=5.4=20; c=7.4=28$ (cm)
27 tháng 8 2021
Bài 3:
a: Xét ΔOCA và ΔOCB có
OC chung
\(\widehat{AOC}=\widehat{BOC}\)
OA=OB
Do đó: ΔOCA=ΔOCB
b: Xét ΔOHA và ΔOHB có
OA=OB
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(1)
Ta có: CB=CA
nên C nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
hay OC\(\perp\)AB
27 tháng 8 2021
Bài 1:
a: Xét ΔCAB và ΔCDE có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó: ΔCAB=ΔCDE
b: Ta có: ΔCAB=ΔCDE
nên \(\widehat{CAB}=\widehat{CDE}\)
mà \(\widehat{CAB}=80^0\)
nên \(\widehat{CDE}=80^0\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DE
NM
2
15 tháng 8 2021
Bài 3:
Ta có: \(2x=3y=4z\)
nên \(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}\)
mà x-y+z=60
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x-y+z}{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}}=144\)
Do đó: x=72; y=48; z=36
NM
1
22 tháng 8 2021
Bài 3:
Gọi số học sinh khối 6,7,8,9 lần lượt là a,b,c,d
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\)
Do đó: a=32; b=48; c=60; d=70
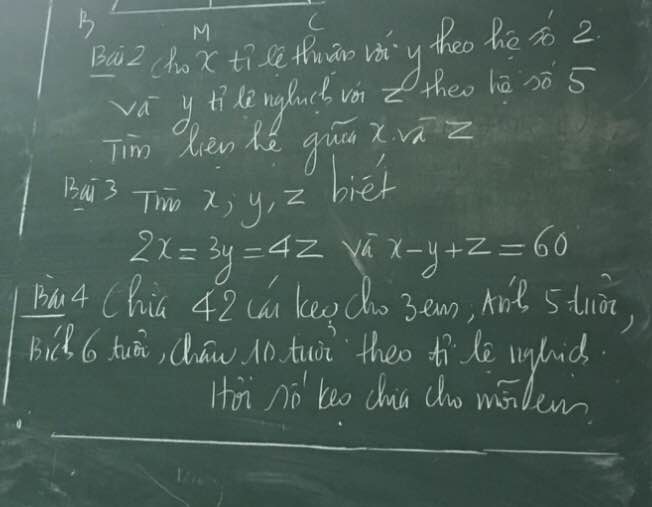
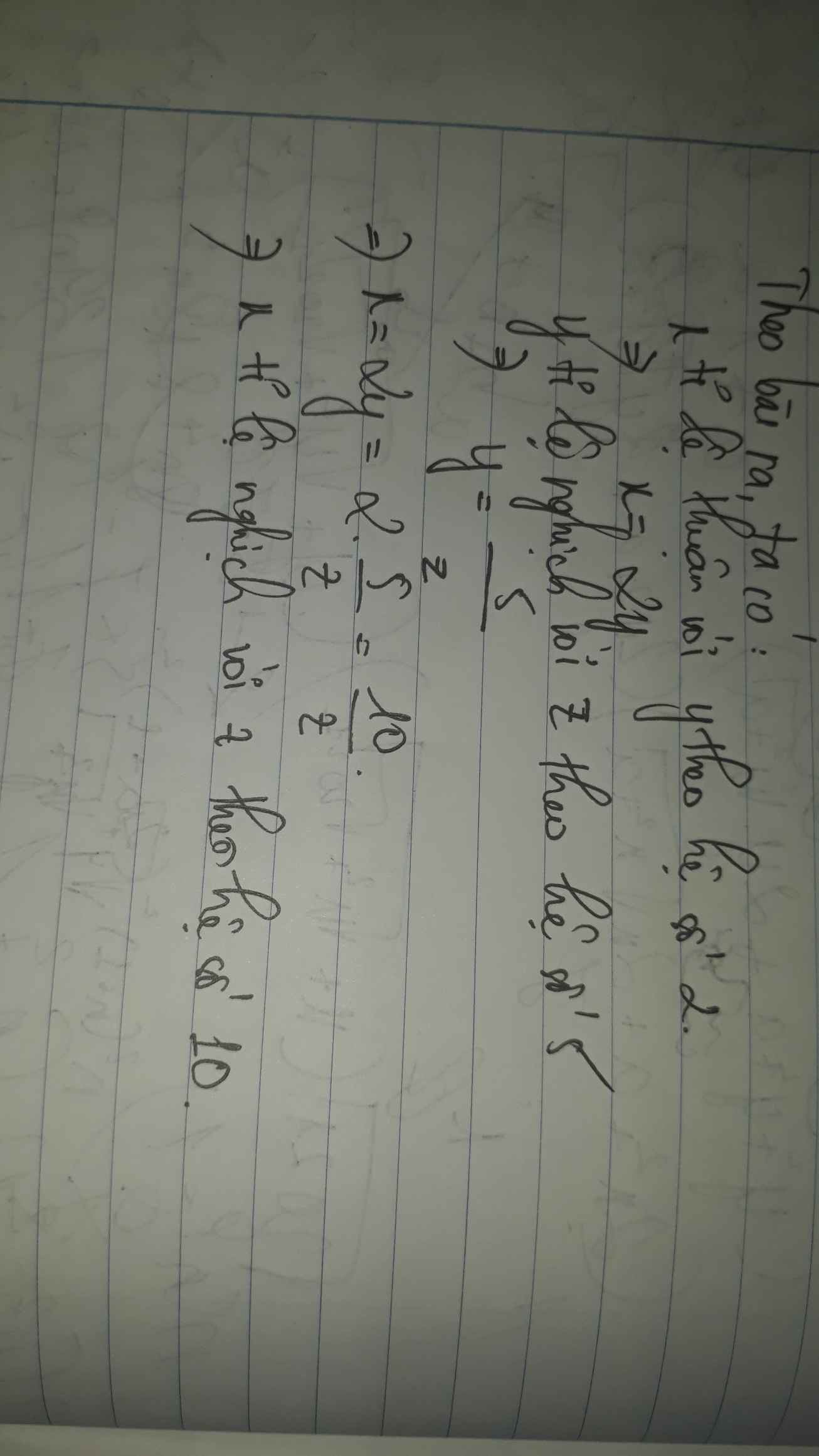
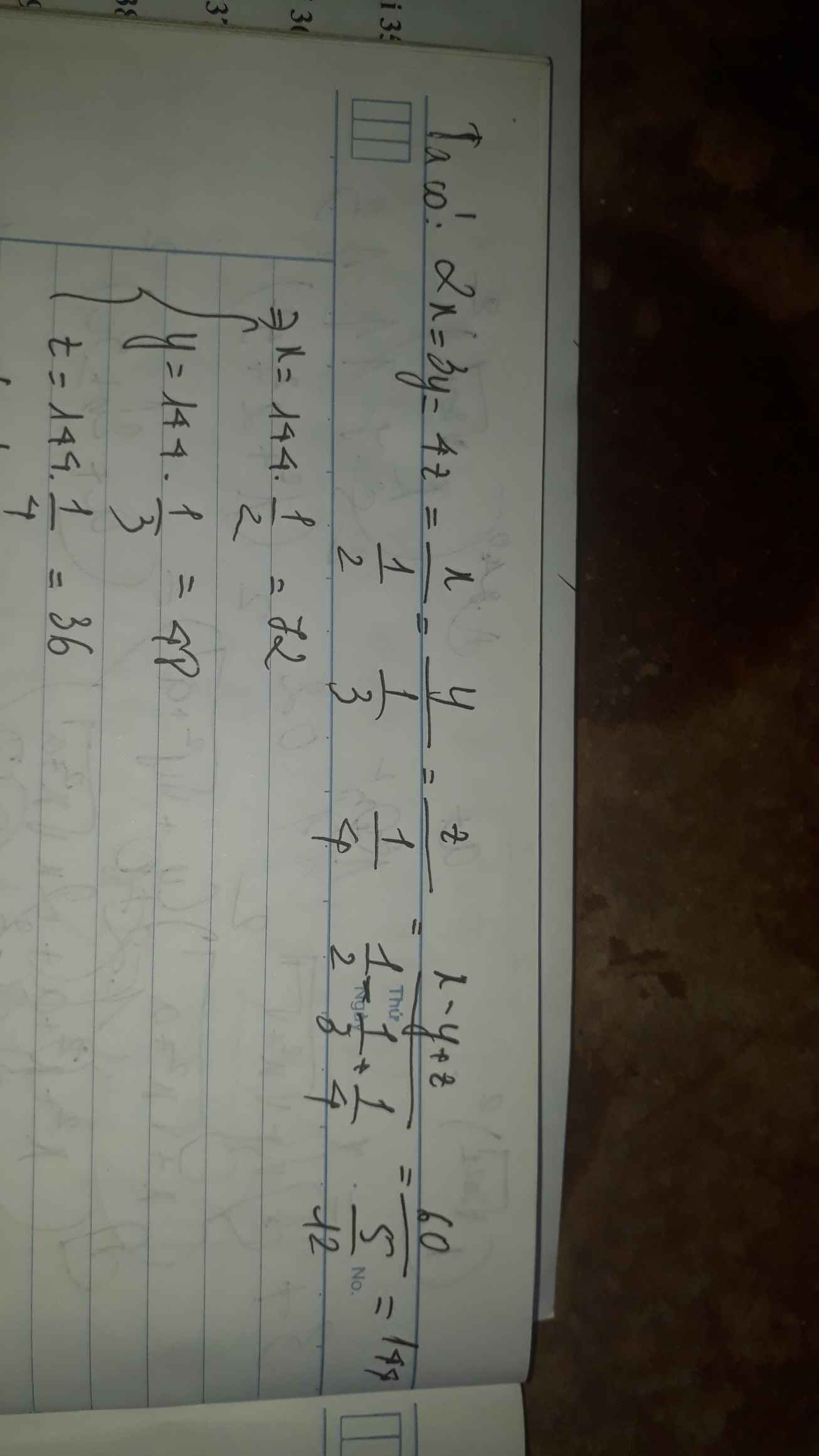
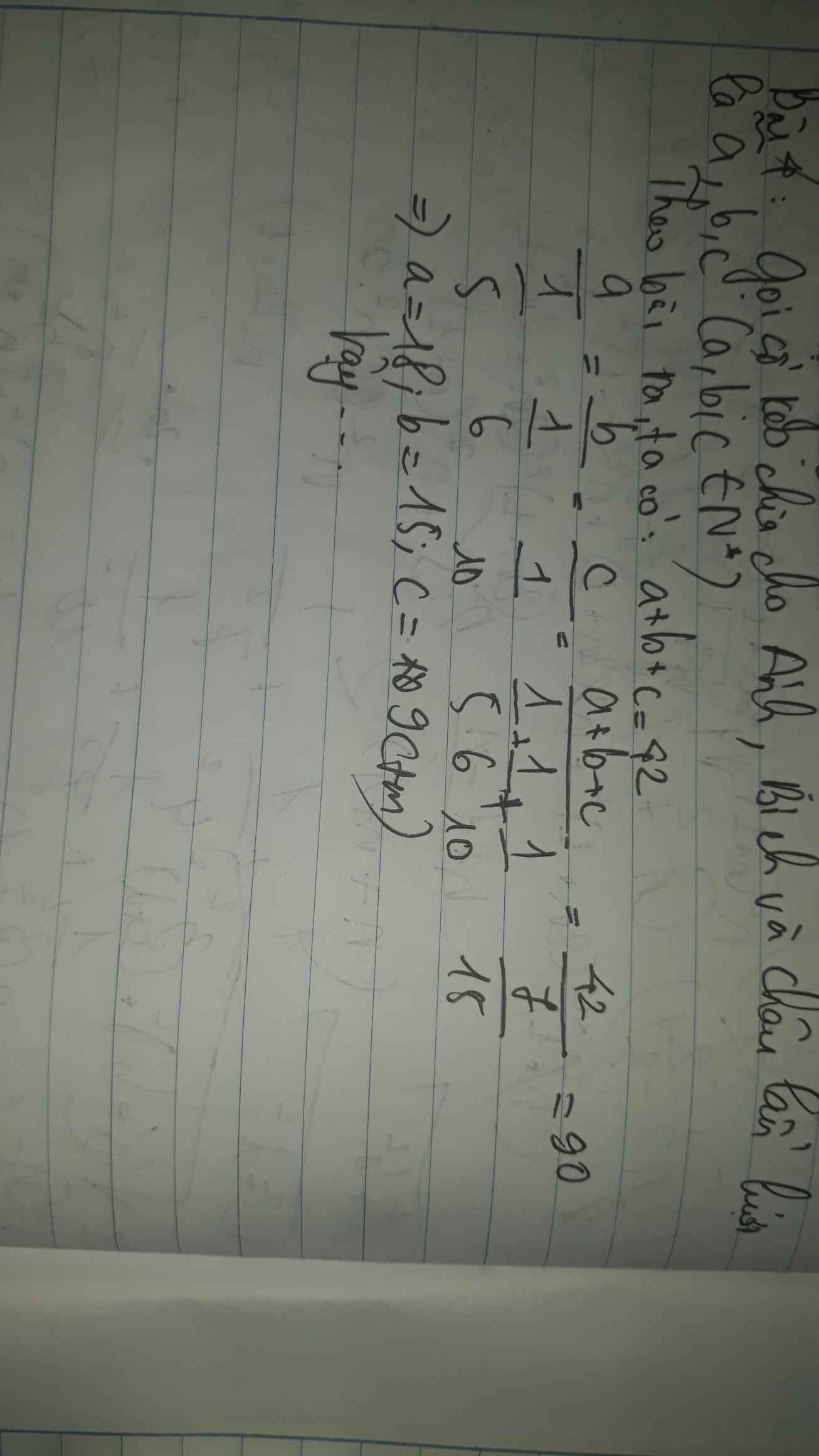
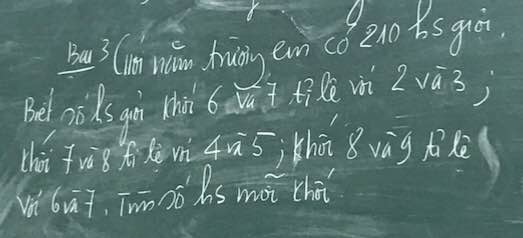
mình làm cho bạn bài 7
vì a,b song song suy và dường thẳng AB cắt a,b tại B,A suy ra hai góc B1 và A trong cùng phía bù nhau
ta có A + B1=180 độ
hay 70 độ + B1=180độ
suy ra B1=180-70=110 độ
tính d1 cũng làm kiểu như vậy áp dụng tính chất hai góc so le trong nhé bạn xem ở trong sách giáo khoa sẽ có ghi tính chất đó