NM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
1
22 tháng 8 2021
Bài 3:
Gọi số học sinh khối 6,7,8,9 lần lượt là a,b,c,d
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\)
Do đó: a=32; b=48; c=60; d=70
14 tháng 4 2022
\(\Leftrightarrow2n+2-5⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{0;-2;4;-6\right\}\)
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Bài 3:
Gọi $a,b,c$ là độ dài ba cạnh tam giác theo thứ tự tăng dần. Theo bài ra ta có:
$\frac{a}{3}=\frac{b}{5}=\frac{c}{7}$ và $c+a-b=20$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a-b+c}{3-5+7}=\frac{20}{5}=4$
$\Rightarrow a=3.4=12; b=5.4=20; c=7.4=28$ (cm)
26 tháng 1 2019
Ko sao,tức cứ đang,có ai cấm âu
Cuộc sống mà
Nội quy chẳng làm cái j âu
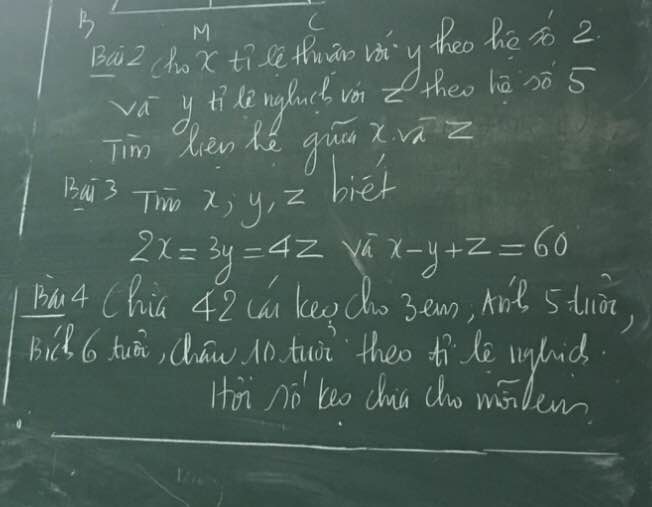
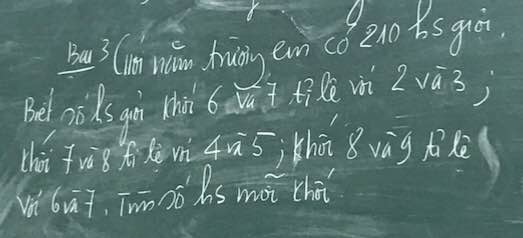
Bài 2:
Bài 3:
Bài 4:
Bài 3:
Ta có: \(2x=3y=4z\)
nên \(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}\)
mà x-y+z=60
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x-y+z}{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}}=144\)
Do đó: x=72; y=48; z=36