
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì \(\hept{\begin{cases}3x=5y\\2y=-3z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{5}=\frac{y}{3}\\\frac{y}{-3}=\frac{z}{2}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\frac{x}{5}=\frac{y}{3}\\\frac{y}{3}=\frac{z}{-2}\end{cases}}\Rightarrow\frac{x}{5}=\frac{y}{3}=\frac{z}{-2}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{x}{5}=\frac{y}{3}=\frac{z}{-2}=\frac{x+y-z}{5+3-\left(-2\right)}=\frac{2}{10}=\frac{1}{5}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{1}{5}.5=1\\y=\frac{1}{5}.3=\frac{3}{5}\\z=\frac{1}{5}.\left(-2\right)=\frac{-2}{5}\end{cases}}\)
Ta có :
\(3x=5y\Leftrightarrow\frac{x}{5}=\frac{y}{3}\)
\(2y=-3z\Leftrightarrow\frac{y}{3}=-\frac{z}{2}\)
Do đó :
\(\frac{x}{5}=\frac{y}{3}=-\frac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{3}=-\frac{z}{2}=\frac{x+y-z}{5+3-2}=\frac{2}{6}=\frac{1}{3}\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{5}=\frac{1}{3}\Rightarrow x=\frac{5}{3}\\\frac{y}{3}=\frac{1}{3}\Rightarrow y=1\\-\frac{z}{2}=\frac{1}{3}\Rightarrow-\frac{2}{3}\end{cases}}\)
Vậy ...

\(\left|2021x+2022\right|+\left|2021x-2021\right|=\left|2021x+2022\right|+\left|2021-2021x\right|\ge\left|2021x+2022+2021-2021x\right|=\left|4043\right|=4043\)
Dấu "=" xảy ra \(\Leftrightarrow\left(2021x+2022\right)\left(2021-2021x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-\dfrac{2022}{2021}\\x\le1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-\dfrac{2022}{2021}\\x\ge1\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow-\dfrac{2022}{2021}\le x\le1\)


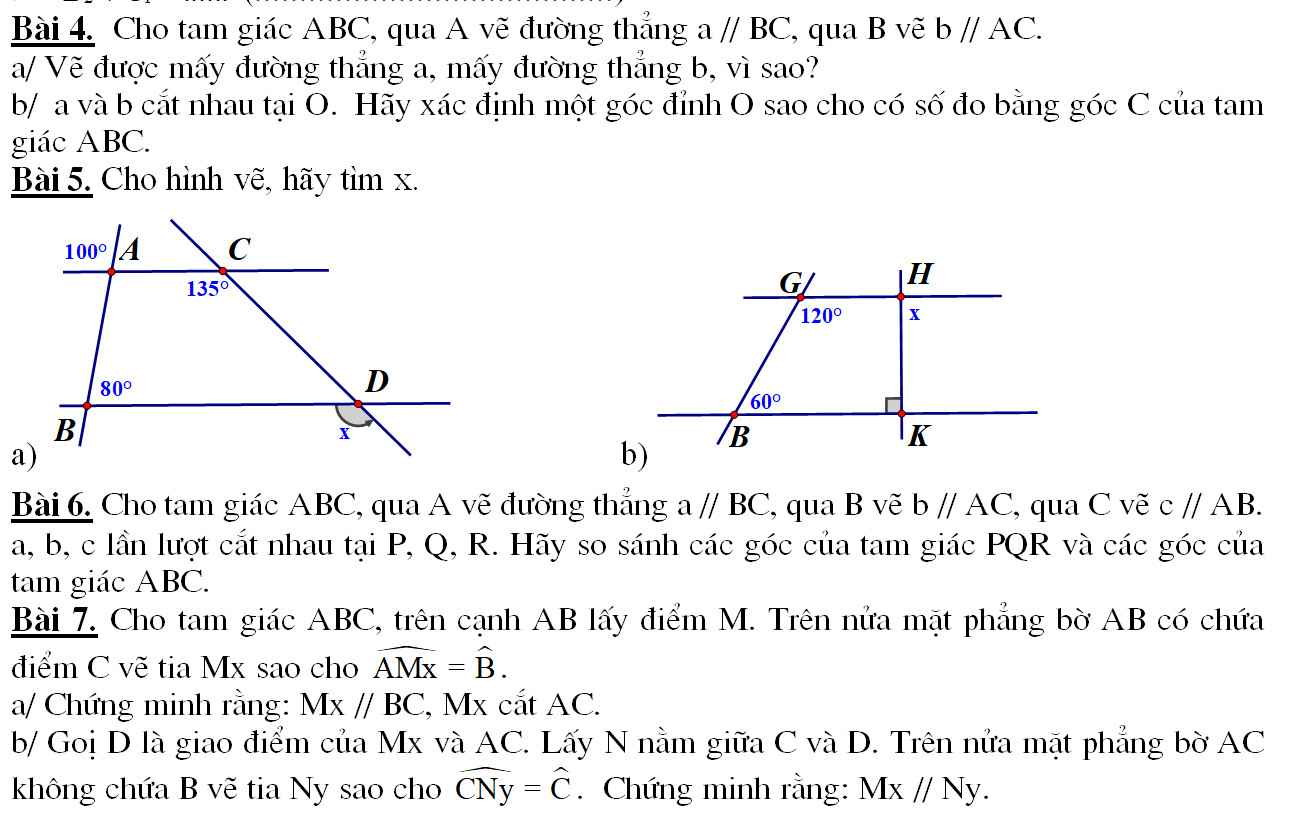
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
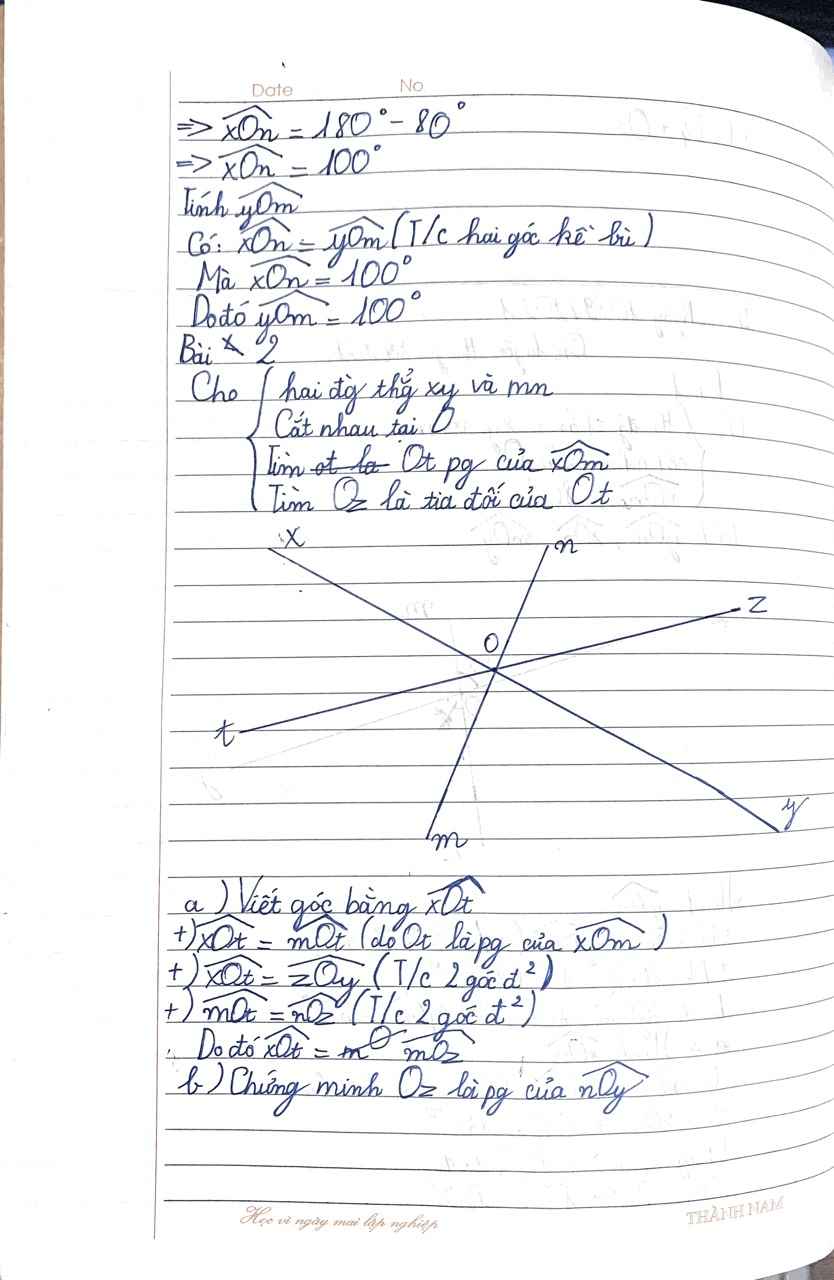
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)


a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
=>BE=CD
Xét ΔEIB vuông tại E và ΔDIC vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó: ΔEIB=ΔDIC
c: Ta có: ΔEIB=ΔDIC
nên IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC

1:
a: Xét ΔBCD vuông tại B và ΔKCD vuông tại K có
CD chung
\(\widehat{BCD}=\widehat{KCD}\)
Do đó: ΔBCD=ΔKCD
Suy ra: BC=KC
=>ΔBKC cân tại C
mà \(\widehat{BCK}=60^0\)
nên ΔBKC đều
b: Ta có: BC=KC
nên C nằm trên đường trung trực của BK(1)
Ta có: DB=DK
nên D nằm trên đường trung trực của BK(2)
Từ (1) và (2) suy ra DC là đường trung trực của BK


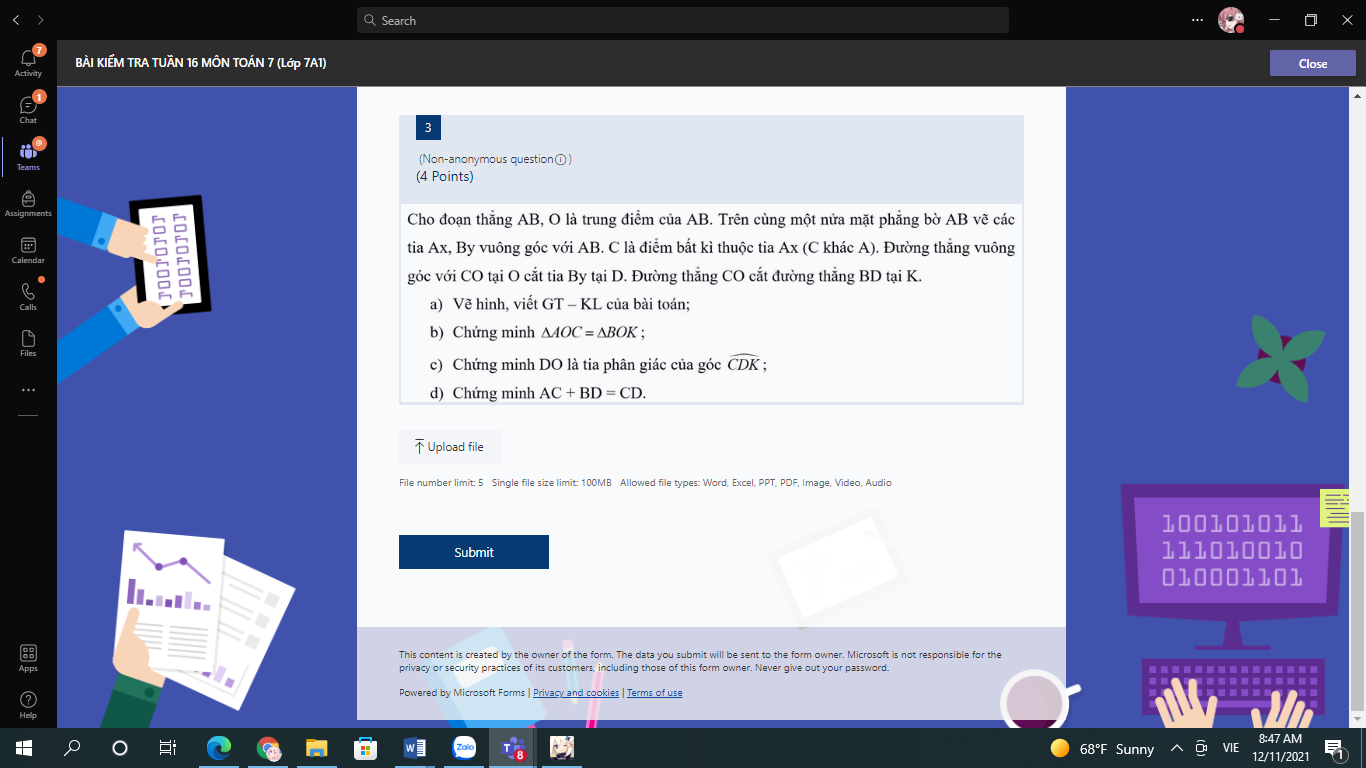

 Giúp mình làm bài này với , mình tick cho .
Giúp mình làm bài này với , mình tick cho .