PD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 3 2022
a: \(\widehat{B}=\dfrac{180^0-80^0}{2}=50^0\)
b: Chiều dài là \(\sqrt{15^2-9^2}=12\left(dm\right)\)
31 tháng 7 2015
M = 22010-(22009 + 22008+....+21+20
Đặt A =( 22009+22008+...21 +20)
Suy ra 2A = 22010+22009+22008+...22+2
Suy ra 2A-A = ( 22010+22009+22008+...+22+2) - (22009+ 22008+...+21+20)
Suy ra A= 22010-20
Suy ra M = 22010-A=22010 - 22010+20=1
Vậy M=1
Đúng nha
25 tháng 7 2021
Bài 11:
a) Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBAD=ΔBED(Cạnh huyền-góc nhọn)
Suy ra: BA=BE(Hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(đpcm)
2 tháng 12 2021
ĐKXĐ : 2x \(\ge\)0 <=> x \(\ge\)0
| 7 + x | = 2x <=> \(\orbr{\begin{cases}7+x=2x\\7+x=-2x\end{cases}}\)
<=> \(\orbr{\begin{cases}x=7\\x=\frac{-7}{3}\end{cases}}\)( KTMĐK)
Vậy x = 7
27 tháng 9 2021
\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)
10 tháng 12 2021
Gọi số đo mỗi cạnh của tam giác lần lượt là x, y, z (đơn vị: m) (x, y, z \(\in\)N*)
Do mỗi cạnh của tam giác tỉ lệ với 4; 5; 8
\(\frac{x}{4}=\frac{y}{5}=\frac{z}{8}\)
Chu vi hình tam giác là 34m
=> x + y + z = 34
Theo tính chất của dãy tỉ số bằng nhau.
\(\frac{x}{4}=\frac{y}{5}=\frac{z}{8}=\frac{x+y+z}{4+5+8}=\frac{34}{17}=2\)
\(\frac{x}{4}=2\Rightarrow x=2.4=8\)
\(\frac{y}{5}=2\Rightarrow y=2.5=10\)
\(\frac{z}{8}=2\Rightarrow z=2.8=16\)
Vậy, độ dài mỗi cạnh của tam giác lần lượt là 8; 10; 16.
@Nghệ Mạt
#cua
10 tháng 12 2021
Gọi các cạnh của tam giác lần lượt là x1, x2, x3
Theo đề bài ta có: \(\frac{x_1}{4}\), \(\frac{x_2}{5}\), \(\frac{x_3}{8}\)= \(\frac{34}{17}\)= \(2\)
Do đó:
x1 = 2.4 = 6
x2 = 2.5 = 10
x3 = 2.8 = 16
Độ dài của các cạnh lần lượt là 6, 10, 16
TG
2
VM
0
25 tháng 9 2021
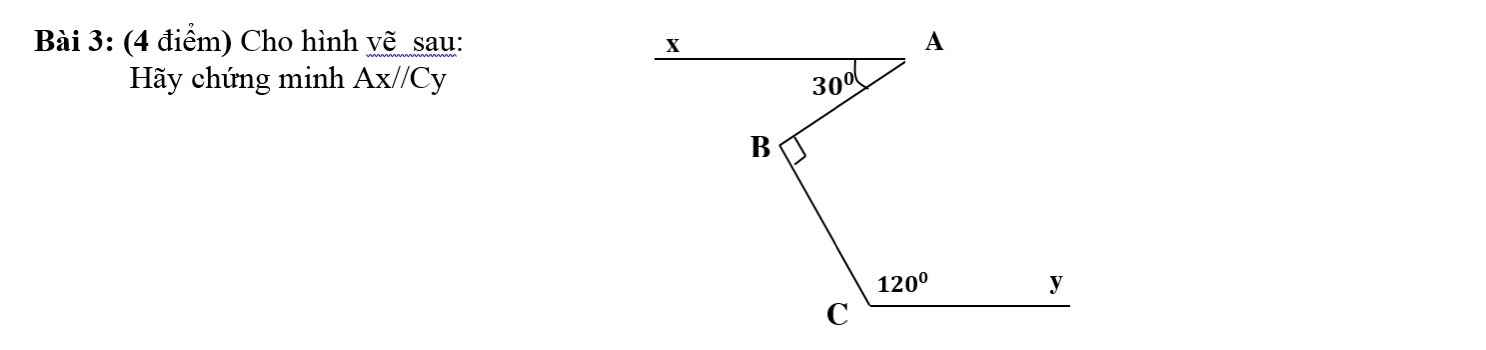
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
Ta dựng đường thẳng CD qua song song với AB, ta có:
\(\widehat{ACD}\) = \(\widehat{A}\) = 400 (so le trong)
\(\widehat{DCE}\) + \(\widehat{ACD}\) = \(\widehat{ACE}\)
⇒ \(\widehat{DCE}\) = \(\widehat{ACE}\) - \(\widehat{ACD}\) = 1000 - 400 = 600
CD // AB ⇒ CD // EG
⇒ \(\widehat{GEx}\) = \(\widehat{DCE}\) (hai góc đồng vị)
⇒ \(\widehat{GEx}\) = 600 (vì hai góc đồng vị)