K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NA
1
30 tháng 7 2023
2:
a: =>x^2(5x^2+2)+2=0
x^2>=0
5x^2+2>=2
=>x^2(5x^2+2)>=0 với mọi x
=>x^2(5x^2+2)+2>=2>0 với mọi x
=>PTVN
b: x^4-12x^2+24=0
=>x^4-12x^2+36-12=0
=>(x^2-6)^2-12=0
=>(x^2-6-2căn 3)(x^2-6+2căn 3)=0
=>x^2=6+2căn 3 hoặc x^2=6-2căn 3
=>\(x=\pm\sqrt{6+2\sqrt{3}};x=\pm\sqrt{6-2\sqrt{3}}\)
29 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\). Gọi \(AB=2x\left(cm\right),AC=3x\left(cm\right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC:
\(BC^2=AB^2+AC^2=4x^2+9x^2=13x^2\)
\(\Rightarrow BC=\sqrt{13}x\)
Xét tam giác ABC vuông tại A có đường cao AH:
\(AH.BC=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow6\sqrt{13}x=6x^2\)
\(\Rightarrow x^2-\sqrt{13}x=0\)
Vì x > 0
\(\Rightarrow x=\sqrt{13}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AB=2x=2\sqrt{13}\left(cm\right)\\AC=3x=3\sqrt{13}\left(cm\right)\\BC=\sqrt{13}x=13\left(cm\right)\end{matrix}\right.\)
29 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\)
nên \(\dfrac{HB}{HC}=\dfrac{4}{9}\)
\(\Leftrightarrow HB=\dfrac{4}{9}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{4}{9}=36\)
\(\Leftrightarrow HC^2=16\)
\(\Leftrightarrow HC=4\left(cm\right)\)
\(\Leftrightarrow HB=9\left(cm\right)\)
Ta có: BH+HC=BC
nên BC=4+9=13(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
27 tháng 6 2023
1: Khi x=25 thì A=(2*5)/(5+2)=10/7
2: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{x-4}=\dfrac{2\left(\sqrt{x}-2\right)}{x-4}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
3: căn x+2>=2
=>P<=2/2=1
Dấu = xảy ra khi x=0
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 8 2021
19.
\(\left(a+b\right)^2\le2\left(a^2+b^2\right)=4\Rightarrow-2\le a+b\le2\)
\(P=3\left(a+b\right)+ab=3\left(a+b\right)+\dfrac{\left(a+b\right)^2-\left(a^2+b^2\right)}{2}=\dfrac{1}{2}\left(a+b\right)^2+3\left(a+b\right)-1\)
Đặt \(a+b=x\Rightarrow-2\le x\le2\)
\(P=\dfrac{1}{2}x^2+3x-1=\dfrac{1}{2}\left(x+2\right)\left(x+4\right)-5\ge-5\) (đpcm)
Dấu "=" xảy ra khi \(x=-2\) hay \(a=b=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 8 2021
20.
Đặt \(P=2a+2ab+abc\)
\(P=2a+ab\left(2+c\right)\le2a+\dfrac{a}{4}\left(b+2+c\right)^2=2a+\dfrac{a}{4}\left(7-a\right)^2\)
\(P\le\dfrac{1}{4}\left(a^3-14a^2+57a-72\right)+18=18-\dfrac{1}{4}\left(8-a\right)\left(a-3\right)^2\le18\) (đpcm)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(3;2;0\right)\)
27 tháng 7 2023
5:
d: \(A=\dfrac{9\left(x_1+x_2\right)+10-3m}{18\left(x_1x_2+2\right)^2+1}\)
\(=\dfrac{9\cdot\dfrac{m-2}{3}+10-3m}{18\cdot\left(\dfrac{m-6}{3}+2\right)^2+1}=\dfrac{3m-6+10-3m}{18\cdot\left(\dfrac{m-6+6}{3}\right)^2+1}\)
\(=\dfrac{4}{18\cdot\dfrac{m^2}{9}+1}=\dfrac{4}{2m^2+1}< =\dfrac{4}{1}=4\)
Dấu = xảy ra khi m=0
12 tháng 8 2021
Bài 1:
a) Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right)\cdot\dfrac{1}{2+\sqrt{2}}\)
=1
b) Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
12 tháng 8 2021
Bài 2:
b) Ta có: \(\sqrt{9x^2-9}+\sqrt{4x^2-4}=\sqrt{16x^2-16}+2\)
\(\Leftrightarrow3\sqrt{x^2-1}+2\sqrt{x^2-1}-4\sqrt{x^2-1}=2\)
\(\Leftrightarrow x^2-1=4\)
\(\Leftrightarrow x\in\left\{\sqrt{5};-\sqrt{5}\right\}\)
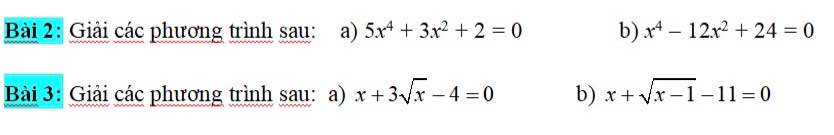
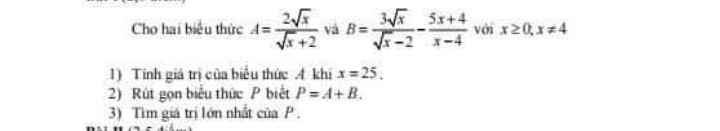
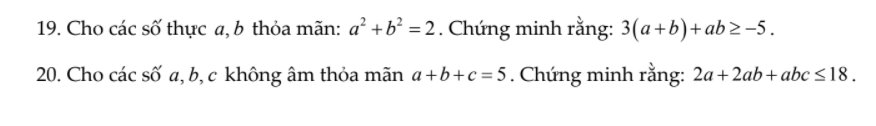
\(a,\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2-4m+3\right)\\ =m^2+2m+1-m^2+4m-3\\ =6m-2\)
Để pt vô nghiệm thì \(6m-2< 0\Leftrightarrow m< \dfrac{1}{3}\)
Để pt có nghiệm kép thì \(6m-2=0\Leftrightarrow m=\dfrac{1}{3}\)
Để pt có 2 nghiệm phân biệt thì \(6m-2>0\Leftrightarrow m>\dfrac{1}{3}\)
\(b,\Delta=\left(m-3\right)^2-4.\left(-3m\right)\\ =m^2-6m+9+12m\\ =m^2+6m+9\\ =\left(m+3\right)^2\ge0\)
Suy ra pt luôn không vô nghiệm với mọi m
PT có nghiệm kép khi \(\left(m+3\right)^2=0\Leftrightarrow m=-3\)
PT có 2 nghiệm phân biệt khi \(\left(m+3\right)^2>0\Leftrightarrow m\ne-3\)