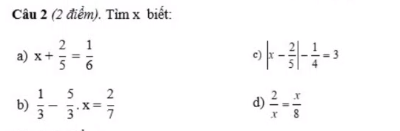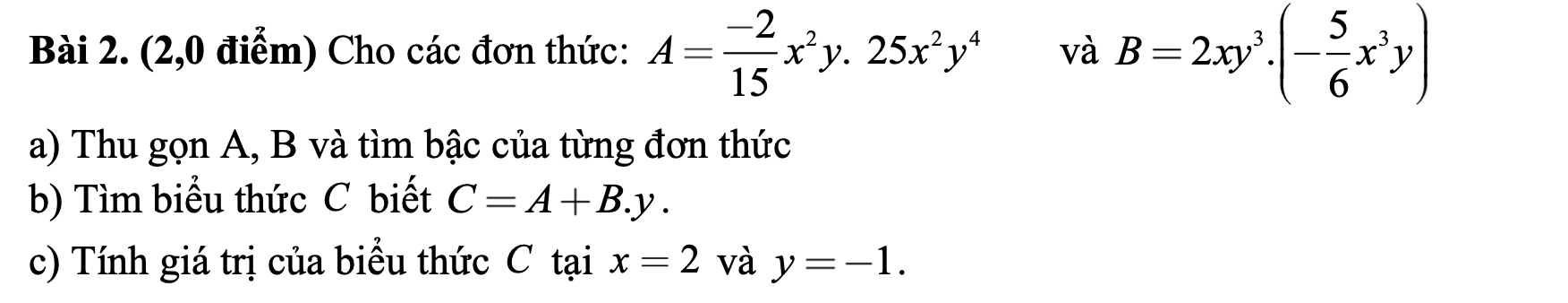K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 8 2021
\(\left\{{}\begin{matrix}x=\dfrac{5}{9}y\\x=\dfrac{10}{21}z\\2x=3y+z=50\end{matrix}\right.\)\(\Rightarrow2x-\dfrac{27}{5}+\dfrac{21}{10}x=50\)
\(\left\{{}\begin{matrix}x=\dfrac{500}{15}\\y=-\dfrac{900}{13}\\-\dfrac{1050}{13}\end{matrix}\right.\)
23 tháng 8 2021
b: Ta có: \(\dfrac{x}{-3}=\dfrac{y}{7}\)
nên \(\dfrac{x}{6}=\dfrac{y}{-14}\left(1\right)\)
Ta có: \(\dfrac{y}{-2}=\dfrac{z}{5}\)
nên \(\dfrac{y}{-14}=\dfrac{z}{35}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}\)
hay \(\dfrac{-2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{-2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}=\dfrac{-2x-4y+5z}{12+56+175}=\dfrac{146}{243}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{292}{81}\\y=-\dfrac{2044}{243}\\z=\dfrac{5110}{243}\end{matrix}\right.\)
NC
1
2D
1
15 tháng 10 2021
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20
W
1
12 tháng 10 2021
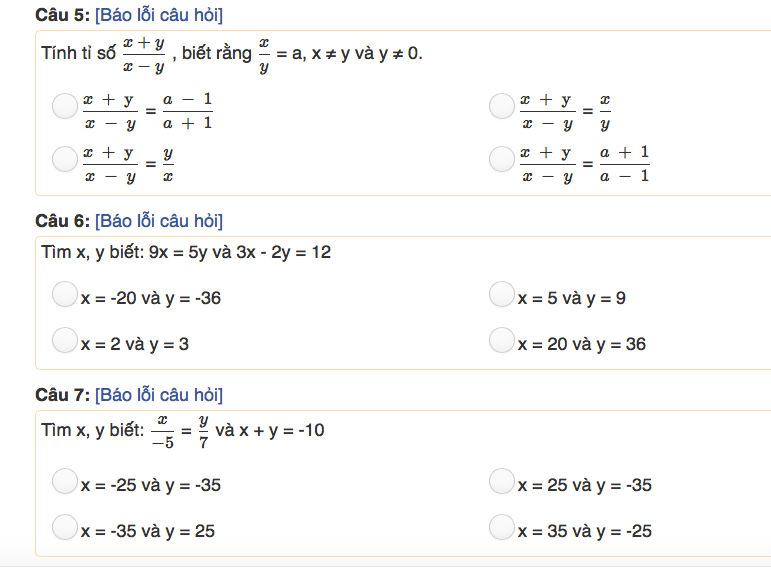
Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)
SK
1
H
5 tháng 11 2021
Câu 2:
\(a,x+\dfrac{2}{5}=\dfrac{1}{6}\) \(b,\dfrac{1}{3}-\dfrac{5}{3}.x=\dfrac{2}{7}\)
\(x=\dfrac{1}{6}-\dfrac{2}{5}\) \(\dfrac{5}{3}.x=\dfrac{1}{3}-\dfrac{2}{7}\)
\(x=-\dfrac{7}{30}\) \(\dfrac{5}{3}.x=\dfrac{1}{21}\)
Vậy \(x=-\dfrac{7}{30}\) \(x=\dfrac{1}{21}:\dfrac{5}{3}\)
\(x=\dfrac{1}{35}\)
Vậy \(x=\dfrac{1}{35}\)
LN
5 tháng 11 2021
a, ⇒ \(x=\dfrac{1}{6}-\dfrac{2}{5}\)
\(\Rightarrow x=\dfrac{5}{30}-\dfrac{12}{30}\)
\(\Rightarrow x=-\dfrac{7}{30}\)
b, \(\Rightarrow\dfrac{5}{3}x=\dfrac{1}{3}-\dfrac{2}{7}\)
⇒ \(\dfrac{5}{3}x=\dfrac{7}{21}-\dfrac{6}{21}\)
\(\Rightarrow\dfrac{5}{3}x=\dfrac{1}{21}\)
\(\Rightarrow x=\dfrac{1}{21}:\dfrac{5}{3}\)
\(\Rightarrow x=\dfrac{1}{21}.\dfrac{3}{5}=\dfrac{1}{35}\)
c, \(\Rightarrow\left|x-\dfrac{2}{5}\right|=3+\dfrac{1}{4}\)
\(\Rightarrow\left|x-\dfrac{2}{5}\right|=\dfrac{13}{4}\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{2}{5}=\dfrac{13}{4}\\x-\dfrac{2}{5}=-\dfrac{13}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{73}{20}\\x=-\dfrac{57}{20}\end{matrix}\right.\)
d, ⇒ x.x = 2.8
⇒ x2 = 16
⇒ x2 = (\(\pm4\))2
⇒ x = \(\pm4\)
ND
1
31 tháng 7 2023
a: A=-2/15*25*x^2y*x^2y^4=-10/3*x^4y^5
B=2*(-5/6)*xy^3*x^3y=-5/3*x^4y^4
b: C=A+B*y
=-10/3*x^4y^5-5/3*x^4y^5
=-5x^4y^5
c: Khi x=2 và y=-1 thì C=-5*2^4*(-1)^5=5*16=80