Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{12}=\frac{y}{-8}=\frac{x+y}{12+\left(-8\right)}=\frac{-48}{4}=-12.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=-12\\\frac{y}{-8}=-12\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-144\\y=96\end{cases}}\)
b ) Từ \(x\):\(\left(-7\right)\)= \(y\): \(10\)
\(\Rightarrow\)\(\frac{x}{-7}=\frac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-7}=\frac{y}{10}=\frac{y-x}{10-\left(-7\right)}=\frac{-34}{17}=-2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-7}=-2\\\frac{y}{10}=-2\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=14\\y=-20\end{cases}}\)
c ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{15}=\frac{y}{-12}=\frac{2x}{30}=\frac{y}{-12}=\frac{2x+y}{30+\left(-12\right)}=\frac{-360}{18}=-20\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=-20\\\frac{y}{-12}=-20\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-300\\y=240\end{cases}}\)
d ) Từ \(2x=-3y\)\(\Rightarrow\)\(\frac{x}{-3}=\frac{y}{2}\)
Áp dugj tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{-3}=\frac{y}{2}=\frac{x}{-3}=\frac{5y}{10}=\frac{x-5y}{-3-10}=\frac{-130}{-13}=10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-3}=10\\\frac{y}{2}=10\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-30\\y=20\end{cases}}\)
Bài 2 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=\frac{x+y-z}{2+\left(-3\right)-5}=\frac{-54}{-6}=9.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=9\\\frac{y}{-3}=9\\\frac{z}{5}=9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=18\\y=-27\\z=45\end{cases}}\)
b ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{-7}=\frac{z}{3}=\frac{x}{4}=\frac{2y}{-14}=\frac{z}{3}=\frac{x+2y-z}{4+\left(-14\right)-3}=\frac{-39}{-13}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{4}=3\\\frac{y}{-7}=3\\\frac{z}{3}=3\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=12\\y=-21\\z=9\end{cases}}\)

a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{90}{10}=9\)
\(\Leftrightarrow\hept{\begin{cases}x=9.2=18\\y=9.3=27\\z=9.5=45\end{cases}}\)
b) \(2x=3y\Leftrightarrow\frac{x}{15}=\frac{y}{10},2y=5z\Leftrightarrow\frac{y}{10}=\frac{z}{4}\)
suy ra \(\frac{x}{15}=\frac{y}{10}=\frac{z}{4}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{4}=\frac{x-z}{15-4}=\frac{11}{11}=1\)
\(\Leftrightarrow\hept{\begin{cases}x=15.1=15\\y=10.1=10\\z=4.1=4\end{cases}}\)
c) \(\frac{x}{y}=\frac{3}{4}\Leftrightarrow\frac{x}{9}=\frac{y}{12},\frac{y}{z}=\frac{3}{5}\Leftrightarrow\frac{y}{12}=\frac{z}{20}\)
suy ra \(\frac{x}{9}=\frac{y}{12}=\frac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{9}=\frac{y}{12}=\frac{z}{20}=\frac{2x-3y+z}{2.9-3.12+20}=\frac{6}{2}=3\)
\(\Leftrightarrow\hept{\begin{cases}x=3.9=27\\y=3.12=36\\z=3.20=60\end{cases}}\)



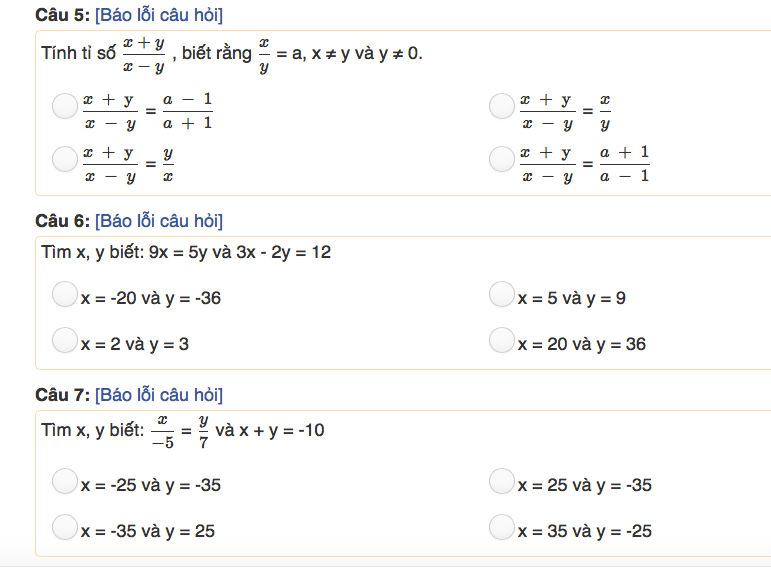










Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)
Cảm ơn bạn nhiều ạ!^^