
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đặt \(log_2x=t\Rightarrow t\ge4\)
Phương trình trở thành: \(\sqrt{t^2-2t-3}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{\left(t+1\right)\left(t-3\right)}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{t+1}=m\sqrt{t-3}\)
\(\Leftrightarrow m=\sqrt{\dfrac{t+1}{t-3}}\)
Hàm \(f\left(t\right)=\sqrt{\dfrac{t+1}{t-3}}\) nghịch biến khi \(t\ge4\)
\(\lim\limits_{t\rightarrow+\infty}\sqrt{\dfrac{t+1}{t-3}}=1\) ; \(f\left(4\right)=\sqrt{5}\)
\(\Rightarrow1< f\left(t\right)\le\sqrt{5}\Rightarrow1< m\le\sqrt{5}\)
Đáp án D

giả sử tổng của số hữu tỉ a vs số vô tỉ b là số hữu tỉ c, ta có b=c-a
mà hiệu của 2 số hữu tỉ phải là số hữu tỉ nên b là số hữu tỉ => mâu thuẫn vs giả thiết
vậy tổng của 1 số hữu tỉ với 1 số vô tỉ là 1 số vô tỉ.
VD : (6+√55) + (6-√55)=12
Có. Ví dụ: (3 - √3) và (2 + √3) là hai số vô tỉ dương, nhưng (3 - √3) + (2 + √3) = 5 là một số hữu tỉ.



\(I=\int\limits^1_0\frac{x^{2\left(n-2\right)}}{\left(1+x^2\right)^n}.xdx\)
Đặt \(1+x^2=t\Rightarrow xdx=\frac{1}{2}dt\)
\(\Rightarrow I=\frac{1}{2}\int\limits^2_1\frac{\left(t-1\right)^{n-2}}{t^n}dt=\frac{1}{2}\int\limits^2_1\left(\frac{t-1}{t}\right)^{n-2}.\frac{1}{t^2}dt=\frac{1}{2}\int\limits^2_1\left(1-\frac{1}{t}\right)^{n-2}.\frac{1}{t^2}dt\)
Đặt \(1-\frac{1}{t}=u\Rightarrow\frac{1}{t^2}dt=du\)
\(\Rightarrow I=\frac{1}{2}\int\limits^{\frac{1}{2}}_0u^{n-2}du=\frac{1}{2\left(n-1\right)}u^{n-1}|^{\frac{1}{2}}_0=\frac{1}{\left(n-1\right)2^n}\)
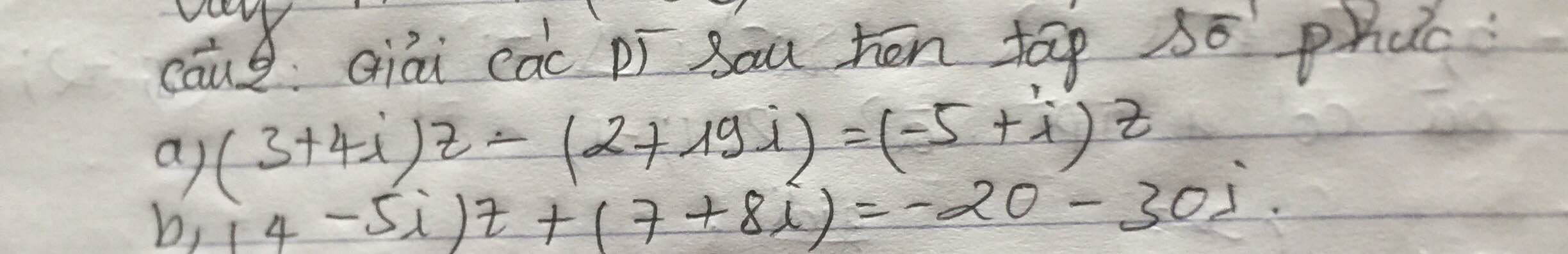

 d
d
Lời giải:
Kẻ \(SH\perp AB\). Do \((SAB)\perp (ABCD)\Rightarrow SH\perp (ABCD)\)
Tam giác $SAB$ đều có đường cao $SH$ nên dễ tính \(SH=\frac{\sqrt{3}a}{2}\)
Kẻ \(HK\perp AD\)
Khi đó, \(\angle ((SAC),(ABCD))=\angle (HK,SK)=\angle HKS=60^0\)
\(\Rightarrow \frac{HK}{HS}=\cot 30^0=\sqrt{3}\Rightarrow HK=\sqrt{3}SH=\frac{3}{2}a\)
Tam giác vuông tại $K$ là $HAK$ có cạnh huyền \(AH=\frac{1}{2}a< HK\) nên bài toán vô lý.