K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
13
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
28 tháng 7 2023
Không biết đây là câu hỏi mẹo hay gì nhỉ? Vì vốn dĩ nó sấp sỉ bằng hoặc có thể là <
QT
Quoc Tran Anh Le
Giáo viên
28 tháng 7 2023
Hãy giải bằng nhiều cách nhất có thể nhé, mỗi cách giải đúng và nhanh nhất mình sẽ cho 1GP nhé. Chấp nhận cách giải mọi cấp bậc học.
VQ
13
14 tháng 8 2023
Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
14 tháng 8 2023
Dễ thấy .
Ta có
Với thì
Vậy , suy ra
Dãy là dãy giảm. Mà có giới hạn hữu hạn. Đặt
Vậy
CM
21 tháng 2 2018
Đáp án B
Cho hai hàm số y=f(x)và y=g(x) liên tục trên [a;b] Khi đó thể tích vật tròn xoay giới hạn bởi hai đồ thị hàm số y=f(x)và y=g(x) và hai đường thẳng x=a; x=b khi quay quanh trục Ox là:
V = π ∫ a b f 2 ( x ) - g 2 ( x ) dx
Cách giải:
Ta có:
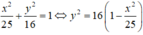
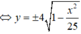
Do tính đối xứng của (H) qua Ox nên thể tích khối tròn xoay cần tìm bằng thể tích khối tròn xoay sinh ra khi quay (H') quanh Ox, trong đó (H') là hình phẳng giới hạn bởi đồ thị hàm số y = 4 1 - x 2 25 và trục Ox.
Xét phương trình hoành độ giao điểm
4 1 - x 2 25 = 0 ⇔ 1 - x 2 25 = 0 ⇔ x 2 = 25 ⇔ x = ± 5
CM
2 tháng 10 2019
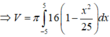
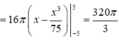
Chọn D.
Phương trình hoành độ giao điểm của đồ thị hàm số y = x2 + x - 1 và y = x4 + x - 1 là :
CM
17 tháng 7 2017
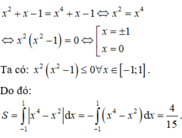
Chọn A.
Ta có: 3 x - 1 ( 3 x + 1 ) 3 x + 1 = 0 ↔ 3 x = 1 ↔ x = 0 . Rõ ràng 3 x - 1 ( 3 - x + 1 ) 3 x + 1 ≥ 0 với mọi x ∈ [0; 1]
Do đó diện tích của hình phẳng là S = ∫ 0 1 3 x - 1 ( 3 - x + 1 ) 3 x + 1 d x = = ∫ 0 1 3 x - 1 ( 3 x + 1 ) 3 x + 1 . 3 x d x
Đặt t = 3 x + 1 , ta có khi x = 0 thì t = 2 , khi x = 1 thì t = 2 và 3x = t2 - 1
Suy ra 3x ln3dx = 2tdt, hay 3 x d x = 2 t d t ln 3 . Khi đó ta có
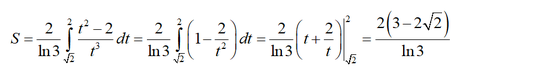
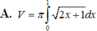
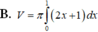
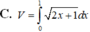
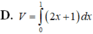
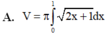
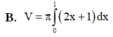
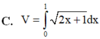
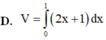
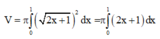
vô ăn hại
= vô hạn