Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dãy số đã cho có thể viết lại là :
\(u_n=\log_{2010}n;n=2,3,4.....\)
Do đó \(a=u_{11}+u_{12}+u_{13}+u_{14}+u_{24}\)
\(=\log_{2010}11+\log_{2010}12+\log_{2010}13+\log_{2010}14+\log_{2010}24\)
\(=\log_{2010}\left(11.12.13.14.24\right)\)
và \(b=u_{63}+u_{64}+u_{65}+u_{66}+u_{67}=\log_{2010}\left(63.64.65.66.67\right)\)
Từ đó suy ra :
\(M=b-a=\log_{2010}\left(63.64.65.66.67\right)-\log_{2010}\left(11.12.13.14.24\right)\)
\(=\log_{2010}\frac{63.64.65}{11.12.13}\)
\(=\log_{2010}\frac{2^7.3^3.5.7.11.13.67}{2^6.3^2.7.11.13}=\log_{2010}\left(2.3.5.67\right)=\log_{2010}2010=1\)

\(logu_1+\sqrt{2+logu_1-2logu_{10}}=2logu_{10}\)
\(\Leftrightarrow logu_1-2logu_{10}+\sqrt{2+logu_1-2logu_{10}}=0\)
\(\Leftrightarrow t^2-2+t=0\)(\(t=\sqrt{2+logu_1-2logu_{10}}\ge0\))
\(\Leftrightarrow\orbr{\begin{cases}t=1\\t=-2\end{cases}}\)
\(\Rightarrow2+logu_1-2logu_{10}=1\)
\(\Leftrightarrow2+logu_1-2log\left(2^9u_1\right)=1\)
\(\Leftrightarrow log\left(10u_1\right)=log\left(2^9u_1\right)^2\)
\(\Rightarrow10u_1=2^{18}u_1^2\)
\(\Leftrightarrow u_1=\frac{10}{2^{18}}\).
\(u_n=\frac{2^{n-1}.10}{2^{18}}>5^{100}\Leftrightarrow n>log_2\left(\frac{5^{100}.2^{19}}{10}\right)=-log_210+100log_25+19\)
Suy ra \(n\ge248\).

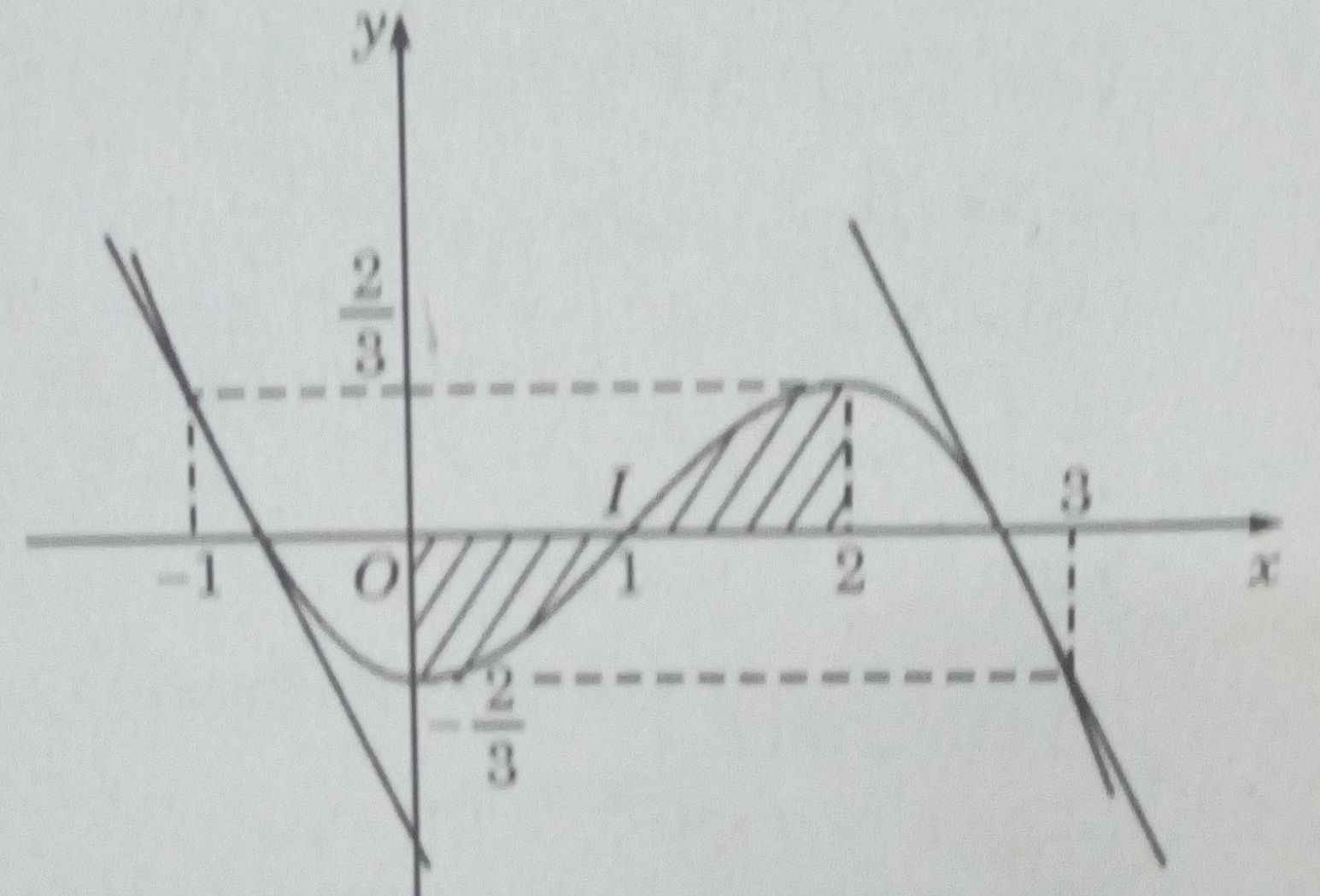
a) Diện tích hình phẳng cần tìm là:
S=2∫−1(x2+1)dx=(x33+x)∣∣2−1=6
b) Diện tích hình phẳng cần tìm là:
S=e∫1e| lnx |dx=e∫1e|lnx|dx+e∫1|lnx|dx=−1∫1elnxdx+e∫1lnxdxS=∫1ee|lnx|dx=∫1ee|lnx|dx+∫1e|lnx|dx=−∫1e1lnxdx+∫1elnxdx
Mặt khác:
∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C
Do đó:
S=−1∫1elnxdx+e∫1lnxdx=1e∫1lnxdx+e∫1xdx=(xlnx−x)∣∣∣1e1+(xlnx−x)∣∣e1=2(1- \(\dfrac{1}{e}\))
Khó quá, làm mà điên não



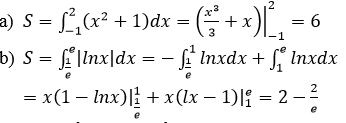

Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
Dễ thấy ��>0,∀�∈N∗un>0,∀n∈N∗.
Ta có ��+1−��=��2+20212��−��=2021−��22��un+1−un=2unun2+2021−un=2un2021−un2
Với �≥2n≥2 thì ��=��−12+20212��−1un=2un−1un−12+2021 =��−12+20212��−1=2un−1+2un−12021 >2��−12.20212��−1>22un−1.2un−12021 =2021=2021
Vậy ��>2021,∀�≥2un>2021,∀n≥2, suy ra ��+1−��=2021−��22��<0,∀�∈N∗un+1−un=2un2021−un2<0,∀n∈N∗
⇒⇒ Dãy (��)(un) là dãy giảm. Mà ��>2021un>2021 ⇒(��)⇒(un) có giới hạn hữu hạn. Đặt lim�→+∞��=�n→+∞limun=L ⇒�=�2+20212�⇒L=2LL2+2021 ⇔�=2021⇔L=2021
Vậy lim�→+∞��=2021n→+∞limun=2021