
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(BH=CH=\dfrac{6}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=5^2-3^2=16\)
=>\(HA=\sqrt{16}=4\left(cm\right)\)
b: Xét ΔAHB có HE là phân giác
nên \(\dfrac{AE}{EB}=\dfrac{AH}{HB}=\dfrac{4}{3}\)(1)
=>\(\dfrac{AE}{4}=\dfrac{EB}{3}\)
mà AE+EB=AB=5cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{4}=\dfrac{EB}{3}=\dfrac{AE+EB}{4+3}=\dfrac{5}{7}\)
=>\(AE=\dfrac{5}{7}\cdot4=\dfrac{20}{7}\left(cm\right)\)
c: Xét ΔAHC có HF là phân giác
nên \(\dfrac{AF}{FC}=\dfrac{AH}{HC}=\dfrac{4}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AF}{FC}\)
Xét ΔABC có \(\dfrac{AE}{EB}=\dfrac{AF}{FC}\)
nên EF//BC
Ta có: EF//BC
BC\(\perp\)AH
Do đó: EF\(\perp\)AH
d: Xét ΔAHB vuông tại H có HE là đường cao
nên \(HE\cdot AB=HA\cdot HB\)
=>\(HE\cdot5=3\cdot4=12\)
=>\(HE=\dfrac{12}{5}=2,4\left(cm\right)\)
Xét ΔABC có EF//BC
nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)
=>\(\dfrac{EF}{6}=\dfrac{20}{7}:5=\dfrac{4}{7}\)
=>\(EF=\dfrac{24}{7}\left(cm\right)\)

Bài 4
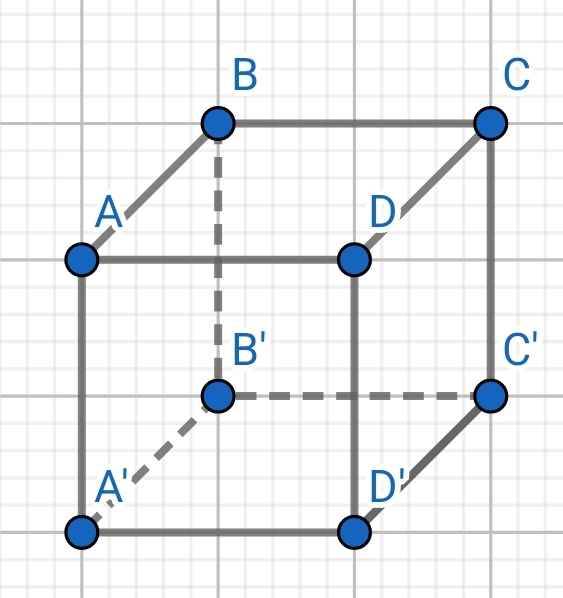
50 mm = 5 cm
Thể tích hình hộp chữ nhật:
V = AB . BC . AA' = 3 . 4 . 5 = 60 (cm³)

b: \(\dfrac{A}{B}=\dfrac{-x^3+5x^2-x-8x^2+40x-8+2}{x^2-5x+1}\)
\(=-x-8+\dfrac{2}{x^2-5x+1}\)


Gọi S(km) là quãng đường để 2 xe gặp nhau(t>0)
Đổi: \(15ph=\dfrac{1}{4}h\)
Theo đề bài ta có: \(\left\{{}\begin{matrix}S=t_1.v_1=15t_1\\S=t_2.v_2=\left(t_1-\dfrac{1}{4}\right).45=-\dfrac{45}{4}+45t_1\end{matrix}\right.\)
\(\Rightarrow15t_1=-\dfrac{45}{4}+45t_1\Rightarrow t_1=\dfrac{3}{8}\left(h\right)\)
Cách điểm a: \(S=t_1.v_1=\dfrac{3}{8}.15=5,625\left(km\right)\)


\(b,=1^2-\left(x-y\right)^2=\left(1+x-y\right)\left(1-x+y\right)\)
\(c,=\left(x^2+1\right)^2-\left(2x\right)^2=\left(x^2+2x+1\right)\left(x^2-2x+1\right)=\left(x+1\right)^2\left(x-1\right)^2\)

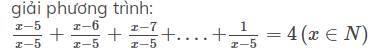 ai đó giúp vớiiiii
ai đó giúp vớiiiii giúp tớ vớiiiii
giúp tớ vớiiiii giúp mình vớiiiii ạ
giúp mình vớiiiii ạ 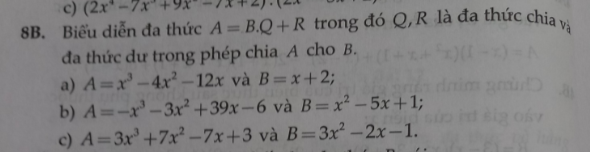


Số số hạng là (1-x+5):1+1=6-x+1=7-x(số)
Tổng là (7-x)*(x-5+1)/2(x-5)
=(7-x)(x-4)/2(x-5)
Theo đề, ta có: (7-x)(x-4)/2(x-5)=4
=>(7x-28-x^2+4x)=8(x-5)
=>-x^2+11x-28-8x+40=0
=>-x^2+3x+12=0
mà x là số tự nhiên
nên \(x\in\varnothing\)