
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tập Trung
Chăm Chỉ
Không hiểu hãy hỏi chứ đừng giấu giốt
Mình đạt 10 năm HS giỏi cho nên biết thế thôi nhé
Yêu bạn
Nắm chắc các lý thuyết, định nghĩa
Không học dồn
Lắng nghe và ghi chép mọi thông tin từ bài giảng
Mạnh dạn hỏi khi chưa hiểu
Đọc trước bài mới ở nhà
Học và làm bài tập thật nhiều
Yêu thích môn học

a.
Lấy $x_1\neq x_2$ là $x_1,x_2\in (1;+\infty)$
Xét \(A=\frac{y(x_1)-y(x_2)}{x_1-x_2}\)
\(y(x_1)-y(x_2)=\frac{2x_1^2-x_1-3}{x_1-1}-\frac{2x_2^2-x_2-3}{x_2-1}=2(x_1-x_2)-(\frac{2}{x_1-1}-\frac{2}{x_2-1})\)
\(=2(x_1-x_2)+\frac{2(x_1-x_2)}{(x_1-1)(x_2-1)}=2(x_1-x_2)[1+\frac{1}{(x_1-1)(x_2-1)}]\)
\(\Rightarrow A=2[1+\frac{1}{(x_1-1)(x_2-1)}]>0\) với $x_1,x_2>1$
Vậy hàm số đồng biến trên TXĐ.
c.
Lấy $x_1\neq x_2\in [-3;+\infty)$
Xét $A=\frac{y(x_1)-y(x_2)}{x_1-x_2}$
\(=\frac{(\sqrt{x_1+5}-\sqrt{x_1+3})-(\sqrt{x_2+5}-\sqrt{x_2+3})}{x_1-x_2}\)
\(=\frac{(\sqrt{x_1+5}-\sqrt{x_2+5})-(\sqrt{x_1+3}-\sqrt{x_2+3})}{x_1-x_2}=\frac{1}{\sqrt{x_1+5}+\sqrt{x_2+5}}-\frac{1}{\sqrt{x_1+3}-\sqrt{x_2}+3}< 0\)
Do đó hàm nghịch biến trên TXĐ.
d. Lấy $x_1\neq x_2\in (-\infty; 0)$
Xét \(A=\frac{y(x_1)-y(x_2)}{x_1-x_2}=\frac{\sqrt{x_1^2+1}-\sqrt{x_2^2+1}}{x_1-x_2}=\frac{x_1^2-x_2^2}{(\sqrt{x_1^2+1}+\sqrt{x_2^2+1})(x_1-x_2)}\)
\(=\frac{x_1+x_2}{\sqrt{x_1^2+1}+\sqrt{x_2^2+1}}<0\) với mọi $x_1,x_2< 0$
Do đó hàm số nghịch biến trên $(-\infty; 0)$
e. Đặt $\sqrt{x+2}=t$ thì ta cần cm hàm:
$y=\frac{2t^2-5}{t}$ đồng biến trên $(0; \sqrt{2})$
Lấy $t_1\neq t_2\in (0;\sqrt{2})$
Xét \(A=\frac{y(t_1)-y(t_2)}{t_1-t_2}=\frac{2t_1-\frac{5}{t_1}-(2t_2-\frac{5}{t_2})}{t_1-t_2}=\frac{2(t_1-t_2)+\frac{5(t_1-t_2)}{t_1t_2}}{t_1-t_2}=2+\frac{5}{t_1t_2}>0\) với mọi $t\in (0;\sqrt{2})$
Vậy hàm số đồng biến.

Câu 1: D
Câu 2: Những mệnh đề sai là: 2,3,4,5,7,8
=>Chọn B
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: D
Câu 7: D
Câu 8: C
Câu 9: D
Câu 10: B

Câu 11: D
Câu 12: D
Câu 13: C
Câu 14: B
Câu 15: C
Câu 16: C
Câu 18: C
Câu 17: A

\(sin\left(\text{α}-\dfrac{\Pi}{4}\right)-cos\left(\text{α}-\dfrac{\Pi}{4}\right)\)
\(=sin\text{α}.cos\dfrac{\Pi}{4}-cos\text{α}-sin\dfrac{\Pi}{4}-\left(cos\text{α}.cos\dfrac{\Pi}{4}+sin\text{α}.sin\dfrac{\Pi}{4}\right)\)
\(=sin\text{α}.\dfrac{\sqrt{2}}{2}-\dfrac{1}{3}.\dfrac{\sqrt{2}}{2}-\dfrac{1}{3}.\dfrac{\sqrt{2}}{2}-sin\text{α}.\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{-2\sqrt{2}}{6}\)
\(=\dfrac{-\sqrt{2}}{3}\)


Bài 9:
\(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}\)
\(=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{CB}\)
\(=\overrightarrow{0}\)



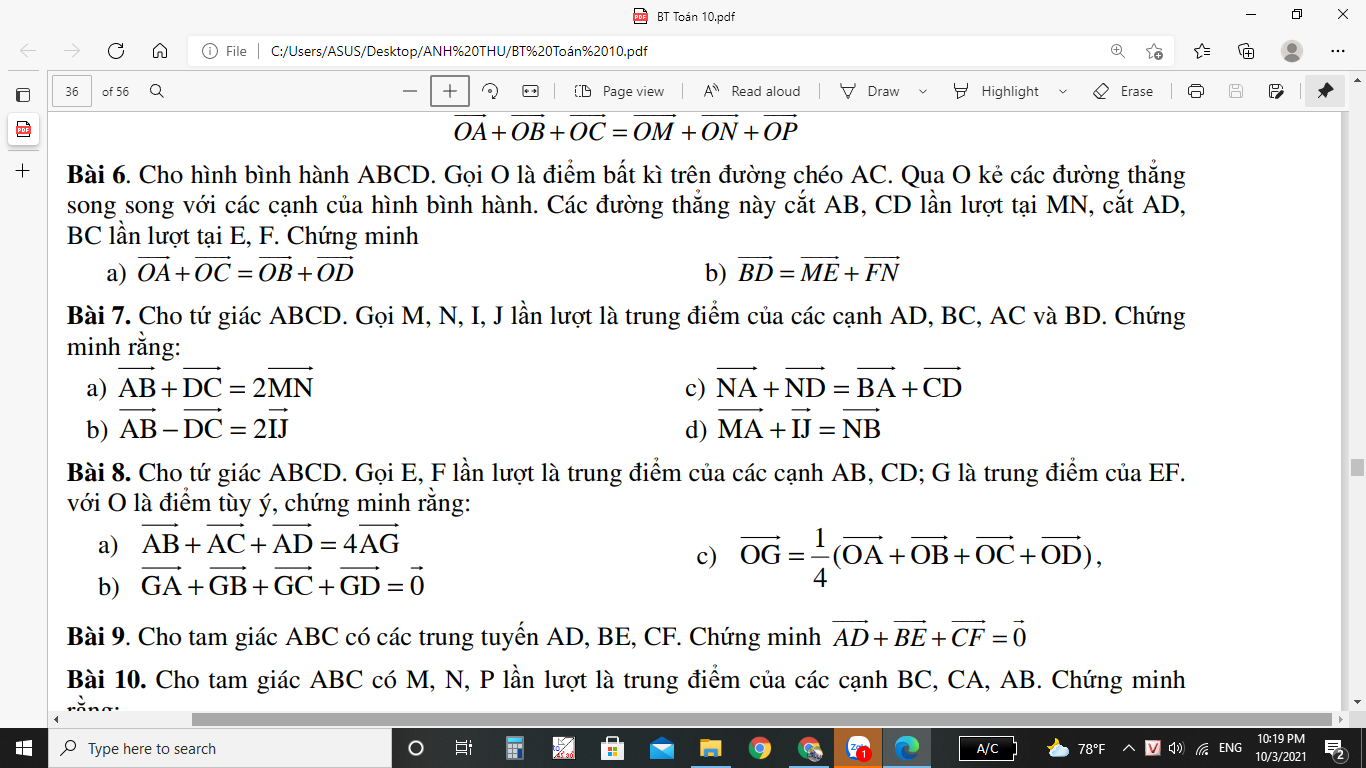 câu 8 làm thế nào vậy mn mình ko bt lm
câu 8 làm thế nào vậy mn mình ko bt lm
Ấn vào.đăng nhập Gmail hoặc iCloud .nhập mật khẩu .thế là xong