
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


thứ 1: Thầy cô ko hiểu
thứ 2: những từ viết tắt có thể bị hiểu sai nghĩa hoặc những từ đó ko cho phép viết tắt
=> không nên viết tắt
![]()


Mỗi bạn có 16 cách viết nên số phần tử không gian mẫu là 16^3.
Gọi A là biến cố '3 số được viết ra có tổng chia hết cho 3'
Các số tự nhiên từ 1 đến 16 chia thành 3 nhóm:
Nhóm I gồm các số tự nhiên chia hết cho 3 gồm 5 số.
Nhóm II gồm các số tự nhiên cho 3 dư 1 gồm 6 số.
Nhóm III gồm các số tự nhiên cho 3 dư 2 gồm 5 số.
Để ba số có tổng chia hết cho 3 thì xảy ra các trường hơp sau:
Cả ba bạn viết được số thuộc nhóm I có 5^3 cách.
Cả ba bạn viết được số thuộc nhóm II có 6^3 cách.
Cả ba bạn viết được số thuộc nhóm III có 5^3 cách.
Mỗi bạn viết được một số thuộc một nhóm có 3!×(5×6×5)
=> n(A) = 5^3 + 6^3 + 5^3 + 3!×(5×6×5) = 1366
Vậy P(A) = 1366/16^3

Không gian mẫu: \(C_{30}^{10}\)
Số cách chọn sao cho 10 học sinh chỉ ở 2 tổ: \(C_{13}^{10}+C_{14}^{10}+C_{15}^{10}+C_{15}^{10}+C_{16}^{10}+C_{17}^{10}\)
Xác suất: \(P=1-\dfrac{C_{13}^{10}+C_{14}^{10}+C_{15}^{10}+C_{15}^{10}+C_{16}^{10}+C_{17}^{10}}{C_{30}^{10}}=...\)


1.
\(y'=\left(cos^2\left(2x+3\right)\right)'=2cos\left(2x+3\right).\left(cos\left(2x+3\right)\right)'\)
\(=2cos\left(2x+3\right).\left(-sin\left(2x+3\right)\right).\left(2x+3\right)'\)
\(=-4sin\left(2x+3\right).cos\left(2x+3\right)\)
\(=-4sin\left(4x+6\right)\)
2.
\(f'\left(x\right)=-x^2+\left(3m-2\right)x-\left(2m^2-5m-2\right)\)
Để \(f'\left(x\right)< 0;\forall x\in R\)
\(\Leftrightarrow\Delta=\left(3m-2\right)^2-4\left(2m^2-5m-2\right)< 0\)
\(\Leftrightarrow m^2+8m+12< 0\)
\(\Rightarrow-6< m< -2\)

\(lim_{n\rightarrow+\infty}\dfrac{6^n+1}{6^n-2}=\)\(lim_{n\rightarrow+\infty}\dfrac{6^n\left(1+\dfrac{1}{6^n}\right)}{6^n\left(1-\dfrac{2}{6^n}\right)}=\)\(lim_{n\rightarrow+\infty}\dfrac{\left(1+\dfrac{1}{6^n}\right)}{\left(1-\dfrac{2}{6^n}\right)}=\dfrac{1}{1}=1\)
\(lim_{n\rightarrow-\infty}\dfrac{6^n+1}{6^n-2}=\)\(\dfrac{0+1}{0-2}=\dfrac{-1}{2}\)
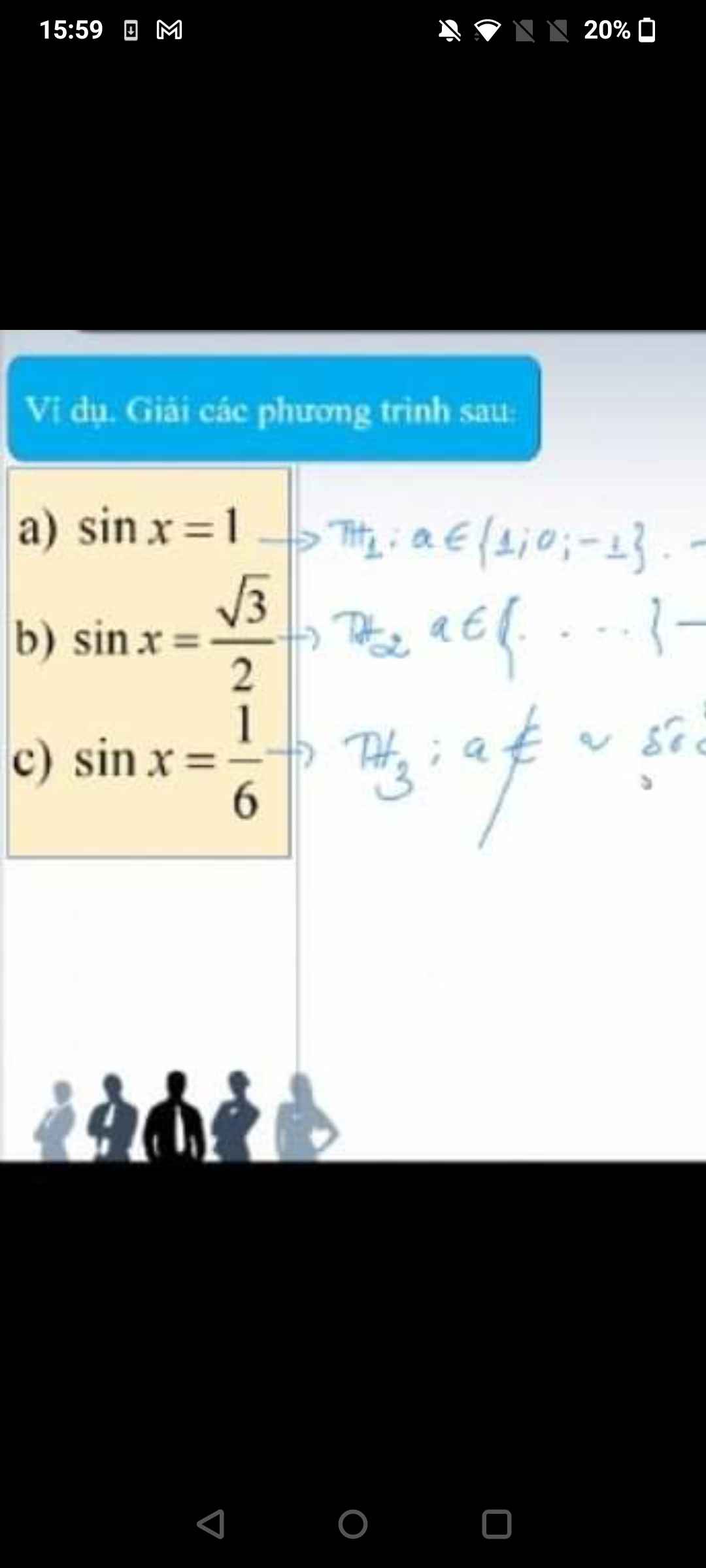



a, \(sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
b, \(sinx=\dfrac{\sqrt{3}}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
c, \(sinx=\dfrac{1}{6}\Leftrightarrow\left[{}\begin{matrix}x=arcsin\dfrac{1}{6}+k2\pi\\x=\pi-arcsin\dfrac{1}{6}+k2\pi\end{matrix}\right.\)