Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D = ( 9 x 2 y 2 – 6 x 2 y 3 ) : ( - 3 x y ) 2 + ( 6 x 2 y + 2 x 4 ) : ( 2 x 2 ) ⇔ D = 9 x 2 y 2 : ( - 3 x y ) 2 – 6 x 2 y 3 : ( - 3 x y ) 2 + 6 x 2 y : ( 2 x 2 ) + 2 x 4 : ( 2 x 2 ) ⇔ D = 1 - 2 3 y + 3 y + x 2 ⇔ D = x 2 + 7 3 y + 1
Đa thức D = x 2 + 7 3 y + 1 có bậc 2
Đáp án cần chọn là: D

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

`a)D` xác định `<=>a-1 ne 0<=>a ne 1`
`b)` Với `a ne 1` có:
`D=([a-1]/[a^2+a+1]-[1-3a+a^2]/[(a-1)(a^2+a+1)]-1/[a-1]).[1-a]/[a^2+1]`
`D=[(a-1)^2-1+3a-a^2-a^2-a-1]/[(a-1)(a^2+a+1)].[-(a-1)]/[a^2+1]`
`D=[a^2-2a+1-1+3a-a^2-a^2-a-1]/[(-a^2-1)(a^2+a+1)]`
`D=[-a^2-1]/[(-a^2-1)(a^2+a+1)]=1/[a^2+a+1]`
`c)` Với `a ne 1` có:
`1/D=1/[1/[a^2+a+1]]=a^2+a+1=(a+1/2)^2+3/4`
Vì `(a+1/2)^2 >= 0 AA a ne 1`
`=>(a+1/2)^2+3/4 >= 3/4 AA a ne 1`
Hay `1/D >= 3/4 AA a ne 1=>1/D _[mi n]=3/4`
Dấu "`=`" xảy ra `<=>a=-1/2` (t/m).


\(=3y\left(2x^2-y\right)-\left(2x^2-y\right)=\left(3y-1\right)\left(2x^2-y\right)\)
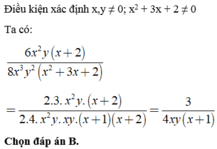
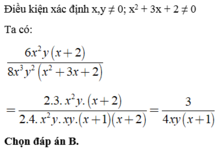
1.\(A=\left(9xy^2-6x^2y\right):\left(-3xy\right)+\left(6x^2y+2x^4\right):2x^2\)
\(=-3xy\left(-3y+2x\right):\left(-3xy\right)+2x^2\left(3y+x^2\right):2x^2\)
\(=-3y+2x+3y+x^2\)
\(=x^2+2x\)
2.Ta có:
\(A=x^2+2x\)
\(=x^2+2x+1-1\)
\(=\left(x+1\right)^2-1\)
Lại có: \(\left(x+1\right)^2\ge0,\forall x\)
\(\Rightarrow\left(x+1\right)^2-1\ge-1\)
Vậy \(Min_A=-1\) khi \(x+1=0\Leftrightarrow x=-1\)