Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Tự vẽ hình) Sửa đề: Phân giác của góc BCD cắt BD tại I
b) Do \(CI\) là phân giác nên ta có: \(\dfrac{IB}{ID}=\dfrac{BC}{CD}\)
Mặt khác: \(\Delta AHB\sim\Delta BCD\) (câu a)
\(\Rightarrow\dfrac{BC}{CD}=\dfrac{AH}{HB}\Rightarrow\dfrac{IB}{ID}=\dfrac{AH}{HB}\Rightarrow IB.HB=ID.AH\)

a) -Xét △AIC và △DIB có:
\(\widehat{IAC}=\widehat{IDB}=90^0\)
\(\widehat{AIC}=\widehat{DIB}\) (đối đỉnh)
\(\Rightarrow\)△AIC∼△DIB (g-g).
\(\Rightarrow\dfrac{AI}{DI}=\dfrac{CI}{BI}\) nên \(\dfrac{AI}{CI}=\dfrac{DI}{BI}\)
b) -Xét △AID và △CIB có:
\(\widehat{AID}=\widehat{CIB}\) (đối đỉnh)
\(\dfrac{AI}{CI}=\dfrac{DI}{BI}\)(cmt)
\(\Rightarrow\)△AID∼△CIB (c-g-c) nên \(\widehat{ABC}=\widehat{ADC}\)
c) -Có: \(\widehat{IAD}=\widehat{ICB}\) (△AID∼△CIB)
\(\widehat{ICA}=\widehat{IBD}\)(△AIC∼△DIB)
Mà \(\widehat{ICB}=\widehat{ICA}\) (CI là tia phân giác của \(\widehat{ACB}\))
\(\Rightarrow\widehat{IAD}=\widehat{IBD}\)
\(\Rightarrow\)△ADB cân tại D nên \(DA=DB\)

a: Xét ΔBCD và ΔYZT có
góc DBC=góc TYZ
góc BCD=góc YZT
=>ΔBCD đồng dạng với ΔYZT
b: ΔBCD đồng dạng với ΔYZT
=>góc BDC=góc YTZ
=>góc BAC=góc YXZ

a, Xét tam giác AHB và tam giác BCD ta có :
^AHB = ^BCD = 900
^BDC = ^ABH ( so le trong )
Vậy tam giác AHB ~ tam giác BCD ( c.g.c )
b, Xét tam giác ADB và tam giác HAD
^A = ^H = 900
^D _ chung
Vậy tam giác ADB ~ tam giác HAD ( g.g )
⇒ADAH=BDAD⇒ADAH=BDAD( tỉ số đồng dạng ) ⇒AD2=BD.DH
c) -Ta có: AD2= DH.DB(cmt)
=> DH= AD2:DB
DH=3^2:5=9:5=1,8
- Xét tam giác BDC vuông tại C có:
DB^2 = BC^2+CD^2
DB^2=3^2+4^2=25
=> BD=5cm
Ta có: tam giác AHB ~ tam giác BCD(CM câu a)
=> AH/BC=AB/BD
=> AH=AB.BC:BD
<=> AH=3.4:5=2,4cm
d) Ta có diện tích tam giác AHB= 1/2 AB.AH=1/2x2,4x4=4.8
Ta có diện tích tam giác BCD= 1/2 BC.DC=1/2x3x4=6
S ABH/ S BCD= 4,8/6=4/5

a: Ta có: \(\widehat{IAB}=\widehat{IDC}\)
\(\widehat{IBA}=\widehat{ICD}\)
mà \(\widehat{IDC}=\widehat{ICD}\)
nên \(\widehat{IAB}=\widehat{IBA}\)
hay ΔIAB cân tại I
b: Xét ΔIBD và ΔIAC có
IB=IA
\(\widehat{BID}\) chung
ID=IC
Do đó: ΔIBD=ΔIAC
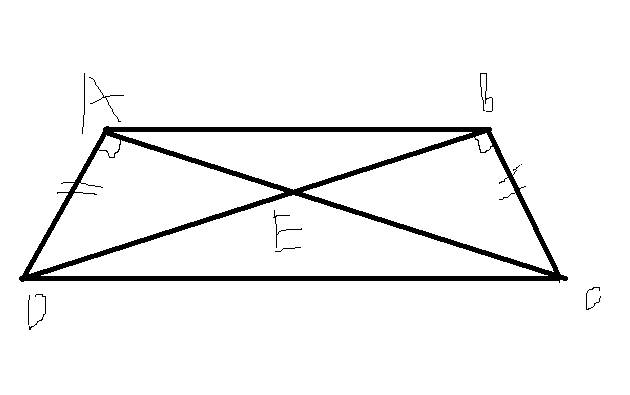
a: Xét ΔADC vuông tại A và ΔBCD vuông tại B có
AD=BC
DC chung
=>ΔADC=ΔBCD
b: ΔADC=ΔBCD
=>góc ACD=góc BDC
=>góc EDC=góc ECD
=>ΔEDC cân tại E
c: Xét ΔEAD vuông tại A và ΔEBC vuông tại B có
ED=EC
AD=BC
=>ΔEAD=ΔEBC
=>EA=EB
Xét ΔEAB và ΔECD có
EA/EC=EB/ED
góc AEB=góc CED
=>ΔEAB đồng dạng với ΔECD
=>góc EAB=góc ECD
=>AB//CD