â ai lam dc help voi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
0
TT
2
28 tháng 8 2016
\(B=\sqrt{8-2\sqrt{5}-\sqrt{8+2\sqrt{5}}}\)
\(B=3,662841501-4,728708045\)
\(B=-1,653330227\)
OT
0
AH
Akai Haruma
Giáo viên
29 tháng 5 2023
Lời giải:
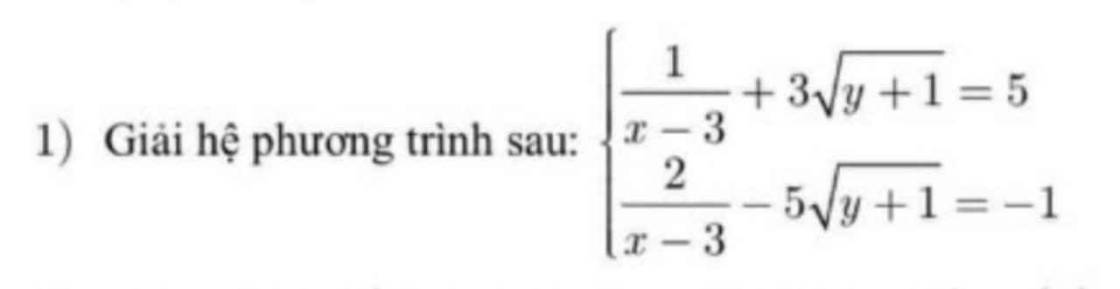
ĐKXĐ: $x\neq 3; y\geq -1$
Đặt $\frac{1}{x-3}=a; \sqrt{y+1}=b(b\geq 0)$ thì hpt trở thành:
\(\left\{\begin{matrix} a+3b=5\\ 2a-5b=-1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a+6b=10\\ 2a-5b=-1\end{matrix}\right.\)
$\Rightarrow (2a+6b)-(2a-5b)=11$
$\Leftrightarrow 11b=11$
$\Leftrightarrow b=1$ (tm)
$a=5-3b=5-3=2$
Khi đó: $(a,b)=(2,1)$
$\Leftrightarrow (\frac{1}{x-3}, \sqrt{y+1})=(2,1)$
$\Leftrightarrow (x,y)=(\frac{7}{2}, 0)$
AH
Akai Haruma
Giáo viên
29 tháng 5 2023
Lời giải:
Đổi 30 phút = 0,5 giờ và 4 giờ 6 phút =4,1 giờ
Gọi vận tốc riêng của cano là $x$ km/h ($x>3$) thì:
Vận tốc xuôi dòng: $x+3$ (km/h)
Vận tốc ngược dòng: $x-3$ (km/h)
Tổng thời gian đi và về:
$\frac{48}{x+3}+\frac{48}{x-3}=4,1-0,5=3,6$
$\Leftrightarrow \frac{1}{x+3}+\frac{1}{x-3}=\frac{3}{40}$
$\Leftrightarrow \frac{2x}{x^2-9}=\frac{3}{40}$
$\Leftrightarrow 3x^2-27-80x=0$
$\Leftrightarrow (x-27)(3x+1)=0$
$\Rightarrow x=27$ (do $x>3$)
Vậy.......
LN
3 tháng 1 2017
bị điếc là hư tai , hư tai là hai tư
vậy đàn chó có 24 con chó.^^
a, \(P=\left(\frac{1}{\sqrt{x}-1}-\frac{2\sqrt{x}}{x\sqrt{x}-x+\sqrt{x}-1}\right):\left(\frac{x+\sqrt{x}}{x\sqrt{x}+x+\sqrt{x}+1}+\frac{1}{x+1}\right)\)
\(=\left(\frac{1}{\sqrt{x}-1}-\frac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right):\left(\frac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(x+1\right)\left(\sqrt{x}+1\right)}+\frac{1}{x+1}\right)\)
\(=\frac{x+1-2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\left(\frac{\sqrt{x}}{x+1}+\frac{1}{x+1}\right)\)
\(=\frac{\left(\sqrt{x}-1\right)^2}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\frac{\sqrt{x}+1}{x+1}\)
\(=\frac{\sqrt{x}-1}{x+1}.\frac{x+1}{\sqrt{x}+1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)(1 )
b, Thay x = 2 vào ( 1 ) ta được :
\(P=\frac{\sqrt{2}-1}{\sqrt{2}+1}\)
c, Thay \(P=\frac{1}{3}\)vào ( 1 ) ta được :
\(\frac{\sqrt{x}-1}{\sqrt{x}+1}=\frac{1}{3}\)
<=> \(3\sqrt{x}-3=\sqrt{x}+1\)
<=> \(2\sqrt{x}=4\)
<=> \(\sqrt{x}=2\)
<=> \(x=4\)