Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.10^{30}=\left(10^3\right)^{10}=1000^{10}\\ 2^{100}=\left(2^{10}\right)^{10}=1024^{10}\)
Vì 100010 < 102410 => 1030 < 2100
\(b,333^{444}=\left(111\cdot3\right)^{444}=111^{444}\cdot3^{444}=111^{444}\cdot81^{111}\\ 444^{333}=\left(111\cdot4\right)^{333}=111^{333}\cdot4^{333}=111^{333}\cdot64^{111}\)
Vì 111444 >111333 ; 81111 > 64111 => 333444 > 444333

số nước cần phải đổ vào bể để bể đầy là
\(1-\frac{3}{4}=\frac{1}{4}\)(bể)
khi mở vòi nước thì số thời gian bể sẽ đầy là \(\frac{1}{4}:\frac{1}{8}=2\)(giờ)
vậy....
12.5* gọi hai số đó là a và b
ta có:a-b=9 (1)
\(\frac{7}{9}a=\frac{28}{33}b\)
=> \(a=\frac{28}{33}b:\frac{7}{9}\)
\(=>a=\frac{12}{11}b\)(2)
thay (2) vào (1) ta đc
\(\frac{12}{11}b-b=9\)
=> \(\frac{1}{11}b=9\)
=>b=99
=> a=99+9=108
vậy...

Trong phép chia , số dư phải bé hơn số chia .
Vậy số dư lớn nhất phải là 6
Giá trị của a là :
16 . 7 + 6 = 118
Vậy a bằng 118
Khi chia cho 7 thì số dư lớn nhất là 6
=>a là:16x7+6=118
P/s:...ko chắc nữa...
~~~~~~~.~~~~~~~~~~~

Gọi số cần tìm là a ( a∈Na∈N ; a≤999a≤999 )
Theo bài ra , ta có :
a : 8 dư 7 => ( a+1 ) ⋮⋮ 8
a : 31 dư 28 => ( a+ 3 ) ⋮⋮ 28
Ta thấy ( a+1 ) + 64 ⋮⋮ 8 = ( a+3 ) +62 ⋮⋮ 31
=> a+65 ⋮⋮ 8 và 31
Mà ( 8;31 ) =1
=> a+65 ⋮⋮ 248
Vì a ≤≤ 999 => a+65 ≤≤ 1064
Để a là số tự nhiên lớn nhất thỏa mãn điều kiện thì cũng phải là số tự nhiên lớn nhất thỏa mãn a+65248=4a+65248=4
=> a=927
Vậy số cần tìm là 927

Bài 1:
a) 3500 = 3100.5 = (35)100 = 243100
5300 = 5100.3 = (53)100 = 125100
Vì 243100 > 125100 nên 3500 > 5300
b) Không thể biết, nếu n > 100 thì thừa lớn hơn, nếu n < 9 thì thừa bé hơn.

Bạn dùng phương pháp chặn `b` rồi tìm `a` nhé.
`8a^2 + 31b^2 = 2468 <=> 31b^2 <= 2468 <=> b^2 < 81 -> b = 1 -> 8.`
Từ đây tìm `a` theo `b` và nhớ thử lại nhé.

Easy mà =)))
Ta thấy: \(\frac{1}{50}>\frac{1}{100}\); \(\frac{1}{51}>\frac{1}{100}\);....;\(\frac{1}{99}>\frac{1}{100}\)
Mà từ 50 - 99 có 50 số nên ta có 50 phân số 100
Cộng theo từng vế,ta được:
\(S=\frac{1}{50}+\frac{1}{51}+...+\frac{1}{99}>\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}=\frac{50}{100}=\frac{1}{2}^{\left(đpcm\right)}\) (do có 50 phân số 1/100)

=>3b(4a-3)+20a-15=2820
=>(4a-3)(3b+5)=2820
=>a chia 4 dư 1, b chia 3 dư 2
Do đó: \(\left(a,b\right)\in\varnothing\)
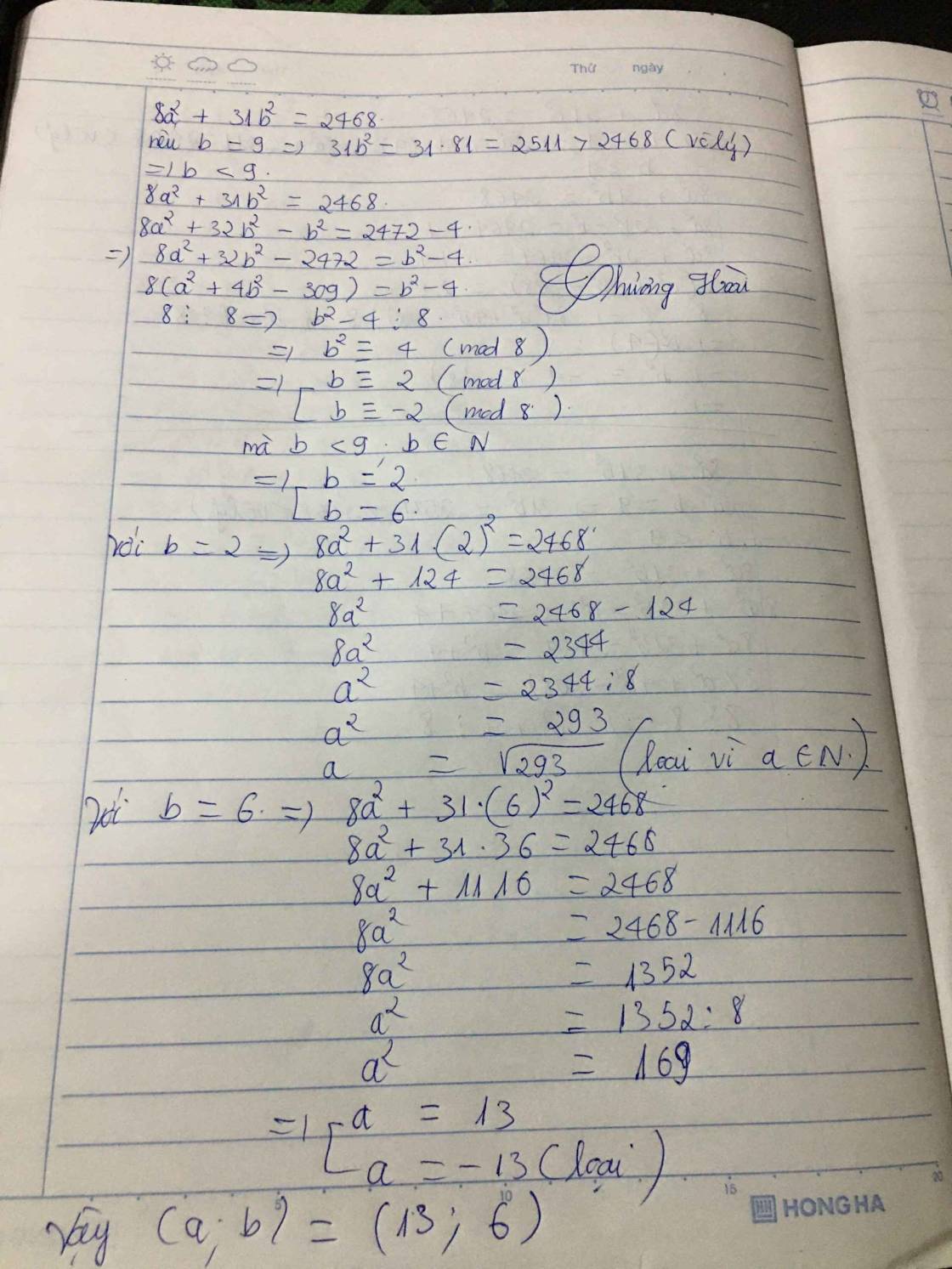
a) 3^200=(3^2)100=9^100
2^300=(2^3)^100=8^100
=>3^200>2^300(vì 9<8)
b) 125^5=(5^3)^5=5^15
25^7=(5^2)^7=5^14
=> 125^5>25^7(vì 15<14)
c) 9^20=(3^2)^20=3^40
27^13=(3^3)^13=3^39
=>9^20>27^13(vì 40<39)
d) 3^54=(3^2)^27=9^27
2^81=(2^3)^27=8^27
=>3^54>2^81(vì 9<8)
e) 10^30=(10^3)^10=1000^10
2^100=(2^10)^10=1024^10
=>10^30<2^100(vì 1000<1024)
f) (5^4)^10=625^10
=>5^40>620^10(vì 625>620)
a) Ta có: \(\hept{\begin{cases}3^{200}=\left(3^2\right)^{100}=9^{100}\\2^{300}=\left(2^3\right)^{100}=8^{100}\end{cases}}\)
Mà \(9^{100}>8^{100}\)=> \(3^{200}>2^{300}\)
b)Ta có: \(\hept{\begin{cases}125^5=\left(5^3\right)^5=5^{15}\\25^7=\left(5^2\right)^7=5^{14}\end{cases}}\)
Mà \(5^{15}>5^{14}\Rightarrow125^5>25^7\)
c) Ta có: \(\hept{\begin{cases}9^{20}=\left(3^2\right)^{20}=3^{40}\\27^{13}=\left(3^3\right)^{13}=3^{39}\end{cases}}\)
Mà: \(3^{40}>3^{39}\Rightarrow9^{20}>27^{13}\)
d) Ta có: \(\hept{\begin{cases}3^{54}=\left(3^2\right)^{27}=9^{27}\\2^{81}=\left(2^3\right)^{27}=8^{27}\end{cases}}\)
Mà: \(9^{27}>8^{27}\Rightarrow3^{54}>2^{81}\)
Còn lại tự làm nha