
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{x^2-x+2m-1}=\sqrt{x-3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x^2-x+2m-1=x-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\f\left(x\right)=x^2-2x+2m+2=0\left(1\right)\end{matrix}\right.\)
Pt có đúng 2 nghiệm pb khi (1) có 2 nghiệm pb thỏa mãn \(3\le x_1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(2m+2\right)>0\\f\left(3\right)=5+2m\ge0\\\dfrac{x_1+x_2}{2}=1>3\left(ktm\right)\end{matrix}\right.\)
Vậy ko tồn tại m thỏa mãn yêu cầu


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn. Viết ntn khá khó đọc.

\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a.cos60^0=\dfrac{a^2}{2}\)
\(\overrightarrow{AB}.\overrightarrow{AM}=AB.AM.cos\widehat{BAM}=a.\dfrac{a\sqrt{3}}{2}.cos30^0=\dfrac{3a^2}{4}\)
\(\overrightarrow{AB}.\overrightarrow{BC}=AB.BC.cos\left(180^0-\widehat{ABC}\right)=a.a.cos120^0=-\dfrac{a^2}{2}\)
\(\overrightarrow{AC}.\overrightarrow{BM}=\overrightarrow{AC}.\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}AC.BC.cos\widehat{ACB}=\dfrac{1}{2}a.a.cos60^0=\dfrac{a^2}{4}\)

6.
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1}\left(x^2-4x+1-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f\left(x\right)=x^2-4x+1-m=0\left(1\right)\end{matrix}\right.\)
a.
Pt có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb lớn hơn 1 hay \(1< x_1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(1-m\right)>0\\f\left(1\right)>0\\\dfrac{x_1+x_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\1-4+1-m>0\\\dfrac{4}{2}>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m< -2\end{matrix}\right.\)
\(\Rightarrow-3< m< -2\)
b.
Pt có đúng 2 nghiệm pb khi (1) có 2 nghiệm pb thỏa mãn \(x_1< 1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=3+m>0\\f\left(1\right)=-2-m< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m>-2\end{matrix}\right.\)
\(\Rightarrow m>-2\)
7.
\(\sqrt{x^2-3x+m}=4-2x\)
\(\Leftrightarrow\left\{{}\begin{matrix}4-2x\ge0\\x^2-3x+m=\left(4-2x\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le2\\3x^2-13x+16-m=0\left(1\right)\end{matrix}\right.\)
a.
Pt có đúng 2 nghiệm pb khi (1) có 2 nghiệm pb thỏa mãn \(x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=13^2-12\left(16-m\right)>0\\f\left(2\right)=2-m\ge0\\\dfrac{x_1+x_2}{2}=\dfrac{13}{6}\le2\left(ktm\right)\end{matrix}\right.\)
Vậy ko tồn tại m thỏa mãn yêu cầu
b.
Pt có nghiệm duy nhất khi (1) có nghiệm kép \(x=-\dfrac{b}{2a}=\dfrac{13}{6}< 2\) (ktm) hoặc có 2 nghiệm pb sao cho \(x_1\le2< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=13^2-12\left(16-m\right)>0\\f\left(2\right)=2-m\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>\dfrac{23}{12}\\m\ge2\end{matrix}\right.\)
\(\Rightarrow m\ge2\)

Để B ⊂ A thì:
1 - 2m ≤ -3 và m + 1 ≥ 5
*) -1 - 2m ≤ -3
⇔ -2m ≤-3 + 1
⇔ -2m ≤ -2
⇔ m ≥ 1 (1)
*) m + 1 ≥ 5
⇔ m ≥ 5 - 1
⇔ m ≥ 4 (2)
Từ (1) và (2) ⇒ m ≥ 4
Vậy m ≥ 4 thì B ⊂ A

Sory Mình ghi nhầm .phải là viết pt C biết tâm của C có tọa độ là những số nguyên á
Gọi I là tâm đường tròn, do (C) qua A và B nên I nằm trên trung trực AB
\(\overrightarrow{AB}=\left(2;2\right)=2\left(1;1\right)\) và \(M\left(2;3\right)\) là trung điểm AB nên pt trung trực d' của AB có dạng:
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)
I thuộc d' nên tọa độ I có dạng: \(I\left(a;5-a\right)\)
\(\Rightarrow\overrightarrow{AI}=\left(a-1;3-a\right)\Rightarrow AI=\sqrt{2a^2-8a+10}\)
Do d tiếp xúc (C) nên \(IA=R=d\left(I;d\right)\)
\(\Leftrightarrow\sqrt{2a^2-8a+10}=\frac{\left|3a+5-a-3\right|}{\sqrt{3^2+1^2}}=\frac{\left|2a+2\right|}{\sqrt{10}}\)
\(\Leftrightarrow20a^2-80a+100=\left(2a+2\right)^2\)
\(\Leftrightarrow16a^2-88a+96=0\Rightarrow\left[{}\begin{matrix}a=\frac{3}{2}\left(l\right)\\a=4\end{matrix}\right.\) \(\Rightarrow I\left(4;1\right)\)
\(\Rightarrow R^2=2a^2-8a+10=10\)
Phương trình (C): \(\left(x-4\right)^2+\left(y-1\right)^2=10\)
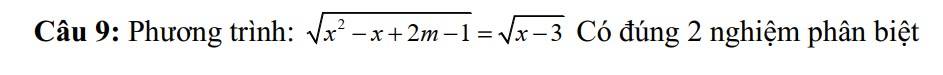 Giúp vớiiii
Giúp vớiiii
 làm giúp mình bài 3 vớiiii :<
làm giúp mình bài 3 vớiiii :< GIÚP TUII VỚIIII! CẢM ƠN NHEEEEE
GIÚP TUII VỚIIII! CẢM ƠN NHEEEEE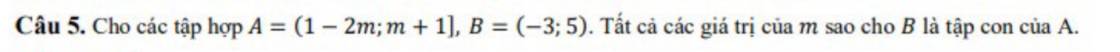
\(\left(-6,6\right)\cdot x+3,4\cdot x+1,2=3,8\\ x\left(-6,6+3,4\right)=3,8-1,2\\ x\cdot\left(-3,2\right)=2,6\\ x=\frac{2,6}{-3,2}=-0,8125\)
Vậy \(x=-0,8125\)