
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)

\(a,A=\left\{0;1;2;3;4\right\}\\ b,B=\left\{-16;-13;-10;-7;-4;-1;2;5;8\right\}\\ c,C=\left\{-9;-8;-7;...;7;8;9\right\}\\ d,x^2-3x+1=0\\ \Delta=9-4=5\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{5}}{2}\\x=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\\ \Leftrightarrow D=\left\{\dfrac{3-\sqrt{5}}{2};\dfrac{3+\sqrt{5}}{2}\right\}\)
\(e,2x^3-5x^2+2x=0\\ \Leftrightarrow x\left(x-2\right)\left(2x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow E=\left\{0;2\right\}\\ f,F=\left\{0;3;6;9;12;15;18\right\}\)

Đáp án C
Ta thấy câu 1), 2) và 4) là các mệnh đề vì ta có thể xét được tính đúng sai của chúng.
Câu 3) không khải mệnh đề vì ta chưa xét được tính đúng sai của nó, chỉ khi cho x một giá trị nào đó thì ta mới nhận được một mệnh đề.
Vậy có 3 mệnh đề.

Đáp án C
Ta thấy câu 1), 2) và 4) là các mệnh đề vì ta có thể xét được tính đúng sai của chúng.
Câu 3) không khải mệnh đề vì ta chưa xét được tính đúng sai của nó, chỉ khi cho x một giá trị nào đó thì ta mới nhận được một mệnh đề.
Vậy có 3 mệnh đề.

Đáp án: D
(x2 - 4) (x2 - 1) = 0 ⇔ x = ±2; x = ±1 nên A = {-2; -1; 1; 2}
(x2 - 4) (x2 + 1) = 0 ⇔ x2 - 4 = 0 ⇔ x = ±2 nên B = {-2; 2}
x4 - 5x2 + 4)/x = 0 ⇔ x4 - 5x2 + 4 = 0 ⇔ x = ±2; x = ±1 nên D = {-2; -1; 1; 2}
=> A = D

5 x 2 + 4 x − x 2 − 3 x − 18 = 5 x 1
ĐK: 5 x 2 + 4 x ≥ 0 x 2 − 3 x − 18 ≥ 0 x ≥ 0 ⇔ x ≥ 0 , x ≤ − 4 5 x ≥ 6 , x ≤ − 3 x ≥ 0 ⇔ x ≥ 6
Khi đó 1 ⇔ 5 x 2 + 4 x = 5 x + x 2 − 3 x − 18
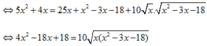
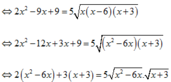
Dễ thấy x = 6 không là nghiệm phương trình nên với x > 6 ta chia cả hai vế cho x 2 − 6 x > 0 ta được:
2 + 3. x + 3 x 2 − 6 x = 5. x + 3 x 2 − 6 x 2
Đặt x + 3 x 2 − 6 x = t > 0 thì (2) trở thành 3 t 2 − 5 t + 2 = 0 ⇔ t = 1 ( T M ) t = 2 3 ( T M )
+ Nếu t = 1 thì x + 3 = x 2 − 6 x
⇔ x + 3 = x 2 − 6 x ⇔ x 2 − 7 x − 3 = 0 ⇔ x = 7 + 61 2 ( T M ) x = 7 − 61 2 ( L )
+ Nếu t = 2 3 thì x + 3 = 2 3 x 2 − 6 x ⇔ x + 3 = 4 9 ( x 2 − 6 x )
⇔ 4 x 2 − 33 x − 27 = 0 ⇔ x = 9 ( T M ) x = − 3 4 ( L )
Vậy phương trình đã cho có tập nghiệm s = 7 + 61 2 ; 9 hay S có 2 phần tử.
Đáp án cần chọn là: D

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
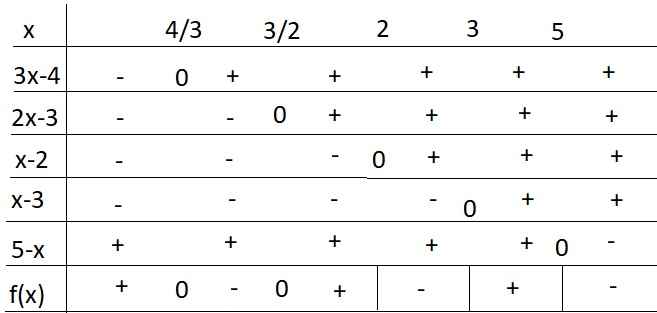
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)