K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
18 tháng 12 2019
Đáp án:B.
Với f(x) = x 3 + 5x + 6 thì vì f'(x) = 3 x 2 + 5 > 0, ∀ x ∈ R nên hàm số f(x) luôn đồng biến trên R. Mặt khác f(-1) = 0. Vậy phương trình f(x) = 0 có nghiệm duy nhất trên R.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 6 2020
\(\overrightarrow{PQ}=\left(-1;-1;4\right)\)
\(\overrightarrow{n_{\left(P\right)}}=\left(3;2;-1\right)\)
\(\Rightarrow\left[\overrightarrow{PQ};\overrightarrow{n_{\left(P\right)}}\right]=\left(-7;11;1\right)\)
\(\Rightarrow\) Mặt phẳng \(\left(\Delta\right)\) nhận \(\left(-7;11;1\right)\) là 1 vtpt
Phương trình:
\(-7\left(x-2\right)+11\left(y-0\right)+1\left(z+1\right)=0\)
\(\Leftrightarrow-7x+11y+z+15=0\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
ĐKXĐ: \(x>3\)
Lấy logarit 2 vế: \(\left(2x^2-7x\right).ln\left(x-3\right)>0\)
\(\Leftrightarrow x\left(2x-7\right)ln\left(x-3\right)>0\)
Bảng xét dấu:
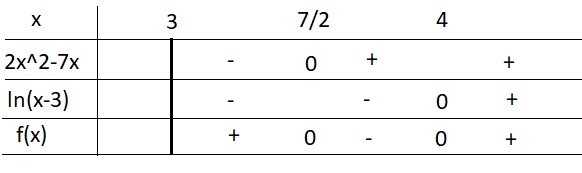
\(\Rightarrow\) Nghiệm của BPT là \(\left[{}\begin{matrix}3< x< \dfrac{7}{2}\\x>4\end{matrix}\right.\)
31 tháng 7 2021
Ta có:\(5^{x-1}\ge5^{x^2-x-9}\)
\(\Leftrightarrow x-1\ge x^2-x-9\)
\(\Leftrightarrow x^2-2x-8\le0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-4\le0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-4\ge0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le4\\x\ge-2\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge4\\x\le-2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow-2\le x\le4\)
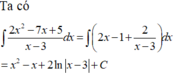
\(5.5^{x-1}+5^2.5^{x-1}+5^{x-1}=7^2.7^{x-1}+7.7^{x-1}+7^{x-1}\Rightarrow31.5^{x-1}=57.7^{x-1}\Rightarrow\left(\frac{7}{5}\right)^{x-1}=\frac{57}{31}\Rightarrow x-1=\log_{\frac{7}{5}}\frac{57}{31}\)