K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
C
10 tháng 1 2023
\(\dfrac{3}{4}-\left[\left(-\dfrac{3}{5}\right)-\left(\dfrac{1}{12}+\dfrac{2}{4}\right)\right]\\ =\dfrac{3}{4}-\left[\left(-\dfrac{3}{5}\right)-\left(\dfrac{1}{12}+\dfrac{6}{12}\right)\right]\\ =\dfrac{3}{4}-\left[\left(-\dfrac{3}{5}\right)-\dfrac{7}{12}\right]\\ =\dfrac{3}{4}-\left[\left(-\dfrac{36}{60}\right)-\dfrac{35}{60}\right]\\ =\dfrac{3}{4}-\left(-\dfrac{71}{60}\right)\\ =\dfrac{3}{4}+\dfrac{71}{60}\\ =\dfrac{35}{60}+\dfrac{71}{60}\\ =\dfrac{106}{60}\\ =\dfrac{53}{30}\)
__
\(-\dfrac{6}{7}.\dfrac{21}{12}\\ =-\dfrac{126}{84}\\ =-\dfrac{63}{42}\\ =-\dfrac{31}{14}\)
__
\(\left(-5\right).\left(-\dfrac{6}{20}\right)\\ =\dfrac{\left(-5\right).\left(-6\right)}{20}\\ =\dfrac{30}{20}\\ =\dfrac{3}{2}\)
__________
NT
1
22 tháng 6 2015
3x-1+5.3x-1=162
=>3x-1.6=162
=>3x-1=162:6
=>3x-1=27=33
=>x-1=3
=>x=4
19 tháng 7 2021
Ta có:
\( \dfrac{7256.4375-725}{3650+4375.7255}\\ =\dfrac{7255.4375+4375-7255}{3650+4375.7255}\\ =\dfrac{7255.4375+\left(4375-725\right)}{3650+4375.7255}\\ =\dfrac{7255.4375+3650}{3650+4375.7255}\\ =1\)
Vậy giá trị của \(\dfrac{7256.4375-725}{3650+4375.7255}=1\)
PT
1
DM
2
20 tháng 9 2023
19/57 . 2 4/7 - 19/57 . 1 5/7 - 19/57
= 19/57 x ( 2 4/7 - 1 5/7 )
= 19/57 x 6/7
= 2/7
20 tháng 9 2023
\(\dfrac{19}{57}.2\dfrac{4}{7}-\dfrac{19}{57}.1\dfrac{5}{7}-\dfrac{19}{57}\)
\(\text{=}\dfrac{19}{57}.\left(2\dfrac{4}{7}-1\dfrac{5}{7}-1\right)\)
\(\text{=}\dfrac{19}{57}.\left(\dfrac{-1}{7}\right)\)
\(\text{=}\dfrac{-1}{21}\)
HV
1
3 tháng 8 2023
a) \(\dfrac{11}{2}=\dfrac{10+1}{2}=5+\dfrac{1}{2}\)
\(\dfrac{32}{9}=\dfrac{27+5}{9}=3+\dfrac{5}{9}< 5+\dfrac{1}{2}\)
Vậy \(\dfrac{11}{2}>\dfrac{32}{9}\)
b)\(\dfrac{100}{23}=\dfrac{92+8}{23}=4+\dfrac{8}{23}\)
\(\dfrac{302}{123}=\dfrac{246+56}{123}=2+\dfrac{56}{123}< 4+\dfrac{8}{23}\)
Vậy \(\dfrac{100}{23}>\dfrac{302}{123}\)
c) \(\dfrac{515}{605}< \dfrac{515+1}{605+1}=\dfrac{516}{606}\Rightarrow\dfrac{515}{605}< \dfrac{516}{606}\)
CM
21 tháng 9 2018
Ta có: 39 = 3. 13 có ước nguyên tố là 13 khác 2 và 5 nên 5/39 có thể viết được dưới dạng số thập phân vô hạn tuần hoàn
Chọn đáp án A
24 tháng 7 2018
a) \(\left|x-1\right|+\left|x+3\right|=4\left(1\right)\)
+) TH1: Nếu \(x< -3\) thì \(x-1< 0;x+3< 0\)
\(\Rightarrow\left|x-1\right|=-x+1;\left|x+3\right|=-x-3\)
PT (1) trở thành: \(-x+1-x-3=4\)
\(\Leftrightarrow-2x=6\Leftrightarrow x=-3\left(loại\right)\)
+) TH2: Nếu \(-3\le x< 1\) thì \(x-1< 0;x+3>0\)
\(\Rightarrow\left|x-1\right|=-x+1;\left|x+3\right|=x+3\)
PT (1) trở thành: \(-x+1+x+3=4\)
\(\Leftrightarrow0x=0\) (luôn đúng)
Kết hợp với đk ta được: \(\Rightarrow-3\le x< 1\)
+) TH3: Nếu \(x\ge1\) thì \(x-1>0;x+3>0\)
\(\Rightarrow\left|x-1\right|=x-1;\left|x+3\right|=x+3\)
PT (1) trở thành: \(x-1+x+3=4\)
\(\Leftrightarrow2x=2\Leftrightarrow x=1\left(t/m\right)\)
Vậy x nằm trong khoảng \(-3\le x\le1.\)
Mấy bài kia làm tương tự.
24 tháng 7 2018
2.
\(\left|x+1\right|+\left|x+2\right|+...+\left|x+10\right|=605x\)(1)
Vì các thừa số ở vế phải của (1) đều không âm nên x không âm. Do đó \(\left|x+1\right|+\left|x+2\right|+...+\left|x+10\right|=\left(x+1\right)+\left(x+2\right)+...+\left(x+10\right)\)
\(\Rightarrow\left(x+1\right)+\left(x+2\right)+...+\left(x+10\right)=605x\)
\(\Rightarrow10x+\dfrac{10\left(10+1\right)}{2}=605x\)
\(\Rightarrow55=595x\)
\(\Rightarrow x=\dfrac{55}{595}=\dfrac{11}{119}\)
Vậy x = \(\dfrac{11}{119}\)
DN
1
NH
0
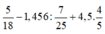
57 + 725 + 605 - 5
= 782 + 600
= 1382
57 + 225 + 605 - 5
= 282 + 605 - 5
= 887 - 5
= 882