K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
20 tháng 1 2019
Ta có: x 2 + 4 x 2 − 4 x − 2 x + k − 1 = 0
⇔ x − 2 x 2 − 4 x − 2 x + k + 3 = 0 ( 1 )
Đặt t = x − 2 x h a y x 2 − t x − 2 = 0 , phương trình trở thành t 2 − 4 t + k + 3 = 0 (2)
Nhận xét: với mỗi nghiệm t của phương trình (2) cho ta hai nghiệm trái dấu của phương trình (1)
Ta có :
∆ ' = 4 - k + 3 = 1 - k ⇒ phương trình (2) có hai nghiệm phân biệt t 1 = 2 − 1 − k , t 2 = 2 + 1 − k với k < 1
+ Với t 1 = 2 − 1 − k thì phương trình x 2 − 2 − 1 − k x − 2 = 0 có 1 nghiệm
x > 1 ⇔ a f ( 1 ) < 0 ⇔ 1 2 − 2 − 1 − k .1 − 2 < 0 ⇔ k > − 8
+ Với t 2 = 2 + 1 − k thì phương trình x 2 − 2 + 1 − k x − 2 = 0 có 1 nghiệm
x > 1 ⇔ a f ( 1 ) < 0 ⇔ 1 2 − 2 + 1 − k .1 − 2 < 0 ⇔ − 3 − 1 − k < 0 (luôn đúng với k < 1 )
Vậy kết hợp điều kiện k < 1 ta được - 8 < k < 1
Đáp án cần chọn là: B
26 tháng 11 2022
a: ĐKXĐ của A là x<>1; x<>-3
ĐKXĐ của B là x<>4
ĐKXĐ của C là x<>0; x<>2
ĐKXĐ của D là x<>3
ĐKXĐ của E là x<>0; x<>2
b: \(A=\dfrac{2x\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{2x}{x-1}\)
Để A=0 thì 2x=0
=>x=0
\(B=\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)^2}=\dfrac{x+4}{x-4}\)
Để B=0 thì x+4=0
=>x=-4
\(C=\dfrac{x\left(x+2\right)}{x\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Để C=0 thì x+2=0
=>x=-2
\(D=\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x+4}{x^2+3x+9}\)
Để D=0 thi x+4=0
=>x=-4
\(E=\dfrac{2x\left(x^2+2x+1\right)}{2x\left(x-2\right)}=\dfrac{\left(x+1\right)^2}{x-2}\)
Để E=0 thì (x+1)^2=0
=>x=-1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow4x^2-1+\sqrt{3x}-\sqrt{x+1}=0\)
\(\Leftrightarrow\left(2x-1\right)\left(2x+1\right)+\dfrac{\left(\sqrt{3x}-\sqrt{x+1}\right)\left(\sqrt{3x}+\sqrt{x+1}\right)}{\sqrt{3x}+\sqrt{x+1}}=0\)
\(\Leftrightarrow\left(2x-1\right)\left(2x+1\right)+\dfrac{2x-1}{\sqrt{3x}+\sqrt{x+1}}=0\)
\(\Leftrightarrow\left(2x-1\right)\left(2x+1+\dfrac{1}{\sqrt{3x}+\sqrt{2x+1}}\right)=0\)
\(\Leftrightarrow2x-1=0\) (do \(2x+1+\dfrac{1}{\sqrt{3x}+\sqrt{x+1}}>0;\forall x\ge0\))
\(\Leftrightarrow x=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
Để pt có 2 nghiệm dương (ko yêu cầu pb?) \(\left\{{}\begin{matrix}a\ne0\\\Delta\ge0\\x_1+x_2=-\frac{b}{a}>0\\x_1x_2=\frac{c}{a}>0\end{matrix}\right.\)
a/ \(\left\{{}\begin{matrix}\Delta=\left(2m-1\right)^2+4m-4\ge0\\x_1+x_2=2m+1>0\\x_1x_2=-m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-3\ge0\\m>-\frac{1}{2}\\m< 1\end{matrix}\right.\) \(\Rightarrow\frac{\sqrt{3}}{2}\le m< 1\)
b/ \(\left\{{}\begin{matrix}\Delta=\left(m+2\right)^2-4\left(-2m+1\right)\ge0\\-m-2>0\\-2m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+12m\ge0\\m< -2\\m< \frac{1}{2}\end{matrix}\right.\) \(\Rightarrow m\le-12\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
e/
\(\left\{{}\begin{matrix}\Delta=\left(m+1\right)^2-4m\ge0\\x_1+x_2=m+1>0\\x_1x_2=m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2\ge0\\m>-1\\m>0\end{matrix}\right.\) \(\Rightarrow m>0\)
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)\ge0\\x_1+x_2=\frac{2\left(3-2m\right)}{m-2}>0\\x_1x_2=\frac{5m-6}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3\ge0\\\frac{3-2m}{m-2}>0\\\frac{5m-6}{m-2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1\le m\le3\\\frac{3}{2}< m< 2\\\left[{}\begin{matrix}m< \frac{6}{5}\\m>2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
CM
20 tháng 8 2019
Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm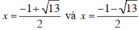 
Ta có bảng xét dấu sau:
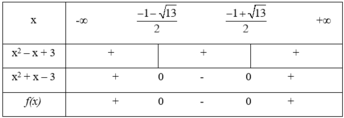
Kết luận:
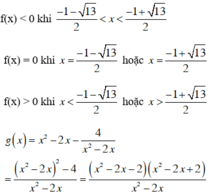
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
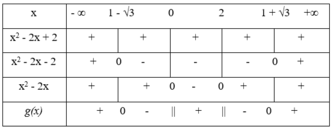
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.
MD
1
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 3 2021
a.
\(\Leftrightarrow2x^2\ge3\Leftrightarrow x^2\ge\dfrac{3}{2}\Rightarrow\left[{}\begin{matrix}x\ge\sqrt{\dfrac{3}{2}}\\x\le-\sqrt{\dfrac{3}{2}}\end{matrix}\right.\)
b.
\(\Leftrightarrow\left(1-x\right)\left(x-3\right)\ge0\Rightarrow1\le x\le3\)
c.
\(\Leftrightarrow\sqrt{1-3x}\le2-x\Leftrightarrow\left\{{}\begin{matrix}1-3x\ge0\\2-x\ge0\\1-3x\le x^2-4x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{3}\\x\le2\\x^2-x+3\ge0\end{matrix}\right.\) \(\Leftrightarrow x\le\dfrac{1}{3}\)
CM
25 tháng 9 2017
Chọn A.
Tam thức -4 x 2 + 5x - 2 có a = -4 <0, Δ = -7 < 0 suy ra -4 x 2 + 5x - 2 < 0, ∀x
Do đó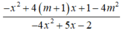 
luôn dương khi và chỉ khi - x 2 + 4(m + 1)x + 1 - 4 m 2 luôn âm
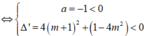
Vậy với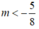 
thì biểu thức 
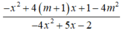luôn dương.
\(\Leftrightarrow\left(4x^2-3x+1\right)^2< \left(x+1\right)^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2-3x+1>-\left(x+1\right)\\4x^2-3x+1< x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2-2x+2>0\\4x^2-4x< 0\end{matrix}\right.\)
\(\Rightarrow0< x< 1\)
NNNNN