K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 10 2023
\(g'\left(x\right)=\left(-2x\right)'\cdot f'\left(-2x\right)\)
\(=-2\cdot f'\left(-2x\right)\)
\(=-2\left(-2x^2-4x\right)\)
\(=4x^2+8x\)
\(g''\left(x\right)=4\cdot2x+8=8x+8\)
g'(x)=0
=>4x(x+2)=0
=>x=0 hoặc x=-2
Khi x=0 thì \(g''\left(x\right)=8\cdot0+8=8\)>0
=>Khi x=0 thì g(x) đạt giá trị cực đại
Khi x=-2 thì \(g''\left(x\right)=8\cdot\left(-2\right)+8=-8< 0\)
=>Khi x=-2 thì g(x) không đạt giá trị cực đại
Vậy: G(x) đạt giá trị cực đại tại x=0
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2022
44.
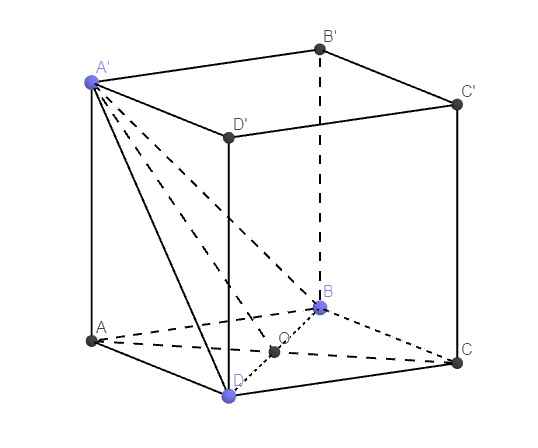
\(AB=\dfrac{BD}{\sqrt{2}}=2a\sqrt{2}\)
Gọi O là giao điểm AC và BD \(\Rightarrow AO\perp BD\Rightarrow BD\perp\left(A'AO\right)\)
\(\Rightarrow\widehat{A'OA}\) là góc giữa (A'BD) và (ABCD)
\(\Rightarrow\widehat{A'OA}=60^0\)
\(\Rightarrow A'A=AO.tan60^0=\dfrac{BD}{2}.tan60^0=2a\sqrt{3}\)
\(\Rightarrow V=A'A.AB^2=16\sqrt{3}a^3\)
15 tháng 2 2020
\(123+54-44+x=x\)
\(\Leftrightarrow123+54-44=0\)
\(\Leftrightarrow177-44=0\)
\(\Leftrightarrow133=0\)( vô lý )
\(\Leftrightarrow x\in\varnothing\)
CM
27 tháng 11 2018
Đáp án D.
y’ = -x2 + 4x + 5
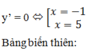
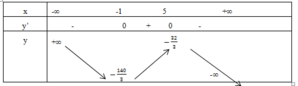
Vậy hàm số đồng biến trên khoảng (-1; 5)
CM
9 tháng 9 2017
+ Điều kiện -4≤x≤4.
Ta thấy hàm số f(x0) liên tục trên đoạn [ -4; 4]
đặt t= x + 4 + 4 - x ⇒ t 2 = x + 4 + 4 - x + 2 ( x + 4 ) ( 4 - x ) ⇒ ( x + 4 ) ( 4 - x ) = t 2 - 8 2
Ta có:
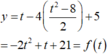
+ Tìm điều kiện của t:
Xét hàm số
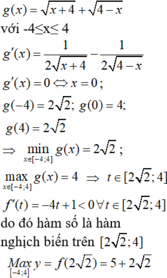
Chọn D.
AH
Akai Haruma
Giáo viên
30 tháng 10 2023
Lời giải:
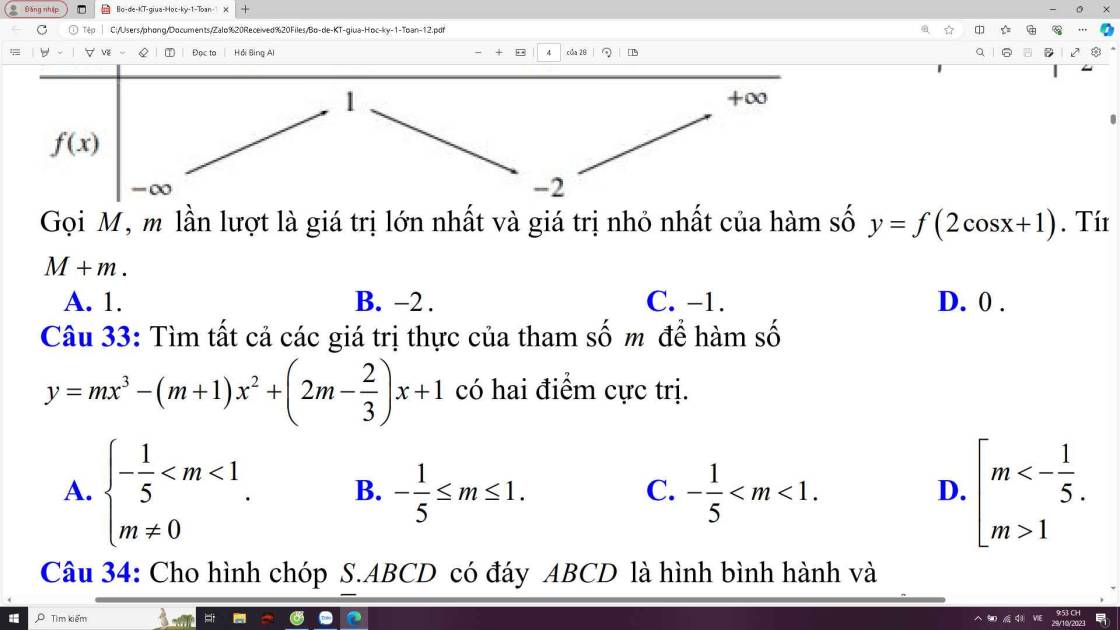
Để $y$ có 2 điểm cực trị thì:
$y'=3mx^2-2(m+1)x+2m-\frac{2}{3}=0$ có 2 nghiệm phân biệt.
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \Delta'=(m+1)^2-3m(2m-\frac{2}{3})>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ -5m^2+4m+1>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ (1-m)(5m+1)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \frac{-1}{5}< m< 1\end{matrix}\right.\)
Đáp án A.
29 tháng 10 2017
Gọi SH là đường cao của hình chóp, có SH=\(\dfrac{a\sqrt{2}}{2}\) \(\Rightarrow\)\(\widehat{SAH}=45^o\)
Đặt MN=x (x>0), có M'H=\(\dfrac{x\sqrt{2}}{2}\)
Có AMM' là tam giác vuông cân nên AM'=MM' = \(\dfrac{a\sqrt{2}}{2}-\dfrac{x\sqrt{2}}{2}\)
\(V_{MNPQ.M'N'P'Q'}=x^2\left(\dfrac{a\sqrt{2}}{2}-\dfrac{x\sqrt{2}}{2}\right)\)
Giả sử cho a=1 ta có \(V=\dfrac{-x^3\sqrt{2}}{2}+\dfrac{x^2\sqrt{2}}{2}\)
Đạo hàm ta đc \(\dfrac{-3\sqrt{2}x^2}{2}+\sqrt{2}x\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy MN=\(\dfrac{2a}{3}\)
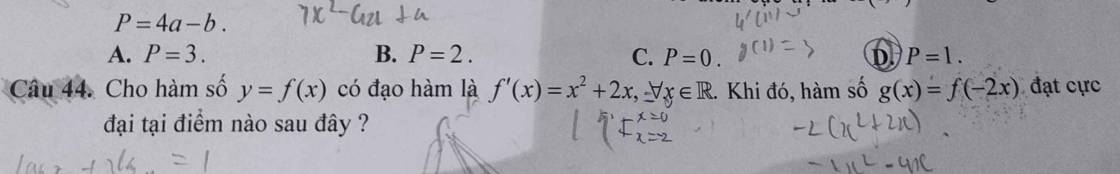
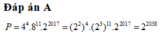
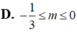
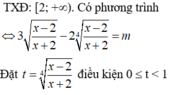
881818833
Đây ko nhắn linh tinh nha bạn
@congtybaocao