Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=3x^2+m+\dfrac{1}{x^6}\ge0\) ; \(\forall x>0\)
\(\Leftrightarrow3x^2+\dfrac{1}{x^6}\ge-m\)
\(\Leftrightarrow-m\le\min\limits_{x>0}\left(3x^2+\dfrac{1}{x^6}\right)\)
Ta có: \(3x^2+\dfrac{1}{x^6}=x^2+x^2+x^2+\dfrac{1}{x^6}\ge4\sqrt[4]{\dfrac{x^6}{x^6}}=4\)
\(\Rightarrow-m\le4\Rightarrow m\ge-4\)

Chọn B.
Hàm số (I): ![]() , ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=> 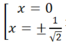 nên hàm số không đồng biến trên khoảng xác định của nó.
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.

Đáp án A.
Tập xác định D = R.
y' = -3x2 + 3
y’ = 0 ⇔ -3x2 + 3 = 0 ⇔ x = 1 hoặc x = -1.
Bảng biến thiên:
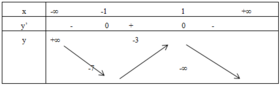
Từ bảng biến thiên ta thấy hàm số đồng biến trên (-1; 1)
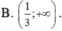
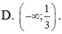

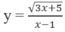 xác định trên R
xác định trên R
Đáp án D.
y’ = -x2 + 4x + 5
Vậy hàm số đồng biến trên khoảng (-1; 5)