K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 6 2017
Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên 1 đường tròn.
4 tháng 6 2017
Một tứ giác nội tiếp có thể được chia nhỏ thành vô số các tứ giác nội tiếp khác.
- Một hình vuông (chữ nhật) có thể chia thành vô số các hình vuông, hình chữ nhật, vốn là các tứ giác nội tiếp.·
- Một hình thang cân có thể chia nhỏ thành vô số các hình thang cân bằng (vô số) các đường thẳng song song với đáy và cắt hai cạnh bên.
- Một tứ giác nội tiếp bất kì cũng có thể được chia thành bốn tứ giác sau:
Từ đa giác nội tiếp lớn ban đầu hãy sắp đặt đa giác sao cho cạnh kề với hai góc nhọn ở dưới. Sau đó kẻ ba đường thẳng song song với ba cạnh để tạo thành hai hình thang cân (1) và (2). Hình thang còn lại, (3), tuy không phải là cân nhưng là tứ giác nội tiếp. Hình (4) có các cạnh song song với tứ giác nội tiếp ban đầu nên đồng dạng và do đó cũng là tứ giác nội tiếp.
Ta có thể áp dụng cách như trên đối với hình (4) để được (vô số) các tứ giác nội tiếp; cũng như phân chia các hình thang cân (1) và (2) thành vô số các hình thang cân (nội tiếp) khác.
Nếu gọi a,b,c,d là độ dài 4 cạnh của tứ giác. p và q là độ dài của hai đường chéo. S là diện tích của tứ giác. R là bán kính đường tròn ngoại tiếp tứ giác. Ta có các công thức:
{\displaystyle {\frac {p}{q}}={\frac {ad+cb}{ab+cd}},\quad p^{2}={\frac {(ac+bd)(ad+bc)}{ab+cd}}\quad {\text{và}}\quad q^{2}={\frac {(ac+bd)(ab+dc)}{ad+bc}}.}
{\displaystyle S={\frac {\sqrt {(ac+bd)(ad+bc)(ab+cd)}}{4R}}\,}
PT
1
TM
3 tháng 5 2023
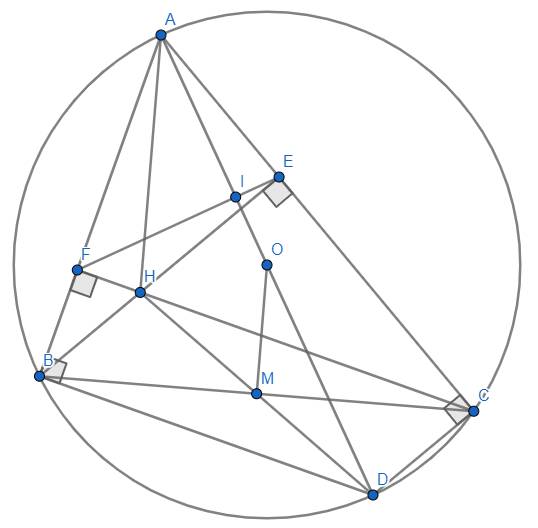
a) \(BE,CF\) là đường cao của \(\Delta ABC\Rightarrow\hat{BFC}=\hat{BEC}=90^o\).
Mà trong tứ giác \(BFEC\), hai góc này có đỉnh kề nhau và cùng nhìn cạnh \(BC\).
Vậy : Tứ giác \(BFEC\) nội tiếp được một đường tròn (dấu hiệu nhận biết) (đpcm).
b) Ta có : \(\hat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AB\perp BD.\)
Mà : \(\hat{BFC}=90^o\left(cmt\right)\Rightarrow AB\perp CF.\)
Từ đó suy ra : \(BD\left|\right|CF\Rightarrow BFCD\) là hình thang.
Mà : \(\hat{BFC}=\hat{ABD}=90^o\left(cmt\right)\Rightarrow BFCD\) là hình thang vuông.
c) Ta có : \(CF\left|\right|BD\left(cmt\right)\) hay \(CH\left|\right|BD\left(1\right).\)
Mặt khác : \(\hat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AC\perp CD\).
Và : \(BE\perp AC\left(gt\right)\)
Suy ra được : \(CD\left|\right|BE\) hay \(CD\left|\right|BH\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BHCD\) là hình bình hành.
Ta cũng có : \(M\) là trung điểm của \(BC\left(gt\right)\Rightarrow M\) cũng là trung điểm của \(HD\left(3\right).\)
Lại có \(O\) là trung điểm của \(AD\left(4\right)\) (tâm đường tròn).
Từ \(\left(3\right),\left(4\right)\Rightarrow OM\) là đường trung bình của \(\Delta HAD\Rightarrow OM=\dfrac{1}{2}AH\Leftrightarrow AH=2.OM\) (đpcm).
d) Cho \(I\) là giao điểm của \(OA\) và \(EF\).
Ta có : \(\hat{ACB}=\hat{ADB}\) (hai góc nội tiếp cùng chắn \(\stackrel\frown{AB}\)).
Hay : \(\hat{ACB}=\hat{BDI}\left(5\right).\)
Mặt khác : Tứ giác \(BFEC\) nội tiếp được một đường tròn (cmt) nên \(\hat{AFI}=\hat{ECB}\) (cùng bù với \(\hat{BFE}\)) hay \(\hat{AFI}=\hat{ACB}\left(6\right).\)
Từ \(\left(5\right),\left(6\right)\Rightarrow\hat{AFI}=\hat{BDI}\) hay \(\hat{AFI}=\hat{ADB}.\)
\(\Delta ABD:\hat{BAD}+\hat{ADB}=90^o\) (hai góc phụ nhau)
\(\Rightarrow\hat{FAI}+\hat{AFI}=90^o.\)
\(\Delta AFI:\hat{FAI}+\hat{AFI}+\hat{AIF}=180^o\) (tổng ba góc trong một tam giác)
\(\Leftrightarrow\hat{AIF}=180^o-\left(\hat{FAI}+\hat{AFI}\right)=180^o-90^o=90^o\)
\(\Rightarrow OA\perp EF\) (đpcm).
CM
4 tháng 5 2019
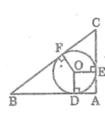
Ta có:
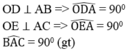
Tứ giác ADOE có ba góc vuông nên nó là hình chữ nhật
Lại có : AD = AE (tính chất hai tiếp tuyến giao nhau)
Vậy tứ giác ADOE là hình vuông
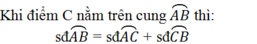
Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên một đường tròn.