K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
19 tháng 6 2017
Thực hiện nhân đa thức và thu gọn
2 n 2 (n + 1) – 2n( n 2 + n – 3) = 6 n ⋮ 6 với mọi giá trị nguyên n.
CM
7 tháng 2 2018
Rút gọn được n 3 – n. Biến đổi thành Q = n(n – 1)(n + 1). Ba số nguyên liên tiếp trong đó sẽ có 1 số chia hết cho 2 và 1 số chia hết cho 3, vì Q ⋮ 6.
CM
9 tháng 5 2017
Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
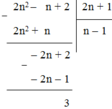
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
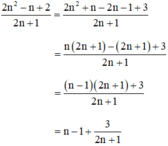
2n2 – n + 2 chia hết cho 2n + 1
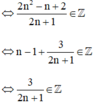
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.
MD
0
DF
1
HH
2 tháng 7 2020
Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
2n2 – n + 2 chia hết cho 2n + 1
<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)
<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }
+ 2n + 1 = 1 <=> 2n = 0 <=> n = 0
+ 2n + 1 = -1 <=> 2n = -2 <=> n = -1
+ 2n + 1 = 3 <=> 2n = 2 <=> n = 1
+ 2n + 1 = -3 <=> 2n = -4 <=> n = -2.
Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }
NV
1
20 tháng 12 2021
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)
15 tháng 12 2021
\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
15 tháng 12 2021
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)
G
2
16 tháng 12 2021
\(A:B=\left(2n^2-4n+3n-6+3\right):\left(n-2\right)\\ =\left[2n\left(n-2\right)+3\left(n-2\right)+3\right]:\left(n-2\right)=2n+3\left(\text{dư }3\right)\)
Để phép chia hết \(\Rightarrow n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow n\in\left\{-1;1;3;5\right\}\)
DT
16 tháng 12 2021
theo đề ta có:
\(\dfrac{A}{B}=\dfrac{2n^2-n-3}{n-2}=\dfrac{2n^2-4n+3n-6+3}{n-2}\)
=\(\dfrac{2n\left(n-2\right)+3\left(n-2\right)+3}{n-2}\)
=\(\dfrac{\left(n-2\right)\left(2n+6\right)}{n-2}=\dfrac{2n+6}{1}=2n+6\)
Vậy đa thức A chia hết cho đa thức B
CM
22 tháng 5 2019
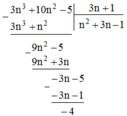
Ta có: 3 n 3 + 10 n 2 - 5 = 3 n + 1 n 2 + 3 n - 1 - 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n =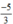 
∉ Z : loại
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n =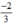 
∉ Z : loại
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n =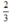 
∉ Z : loại
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì 3 n 3 + 10 n 2 - 5 chia hết cho 3n + 1.
19 tháng 10 2021
Bài 3:
Ta có: \(2n^2+n-7⋮n-2\)
\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)
1n thôi ạ
3n3 + 2n2 + nn
= 3n3 + 2n2 + n2
= 3n3 + 3n2
= 3(n3 + n2)
Nếu n = SC thì sau khi tính xong n3 và n2 , chia nó làm 2 + ... mỗi bên , rồi áp dụng n(a + b) = na + nb , ta x 3 mỗi cái vì có chỗ 3(....). Mà 2 x 3 = 6 nên n = SC sẽ \(⋮6\).
Nếu n = SL thì n3 + n2 = SC , rồi như n = SC , 2 x 3 = 6 nên n = SL sẽ \(⋮6\).
=> 3n3 + 2n2 + nn \(⋮6\)